Generic Elements

B2000++ elements are always derived from one of the generic elements, i.e. an element of a specific family, like a triangle, a tetrahedron, etc. The generic element type is not associated to any operator and is usually known to all processors dealing with elements, like the input processor, the load processor, or the element processor. Like the generic element type, the element name must be derived from the generic element name. The element naming convention

sn.extension

has been adopted, where s designates the shape, n the number of nodes defining the element, and extension the actual description of the element, which also defines the operator. The table below contains a list of all defined generic element types:

Generic element names and properties

Name	x	Description
Lx	2, 3	Line or wire element. Generic 1D element, defined in R3.
Rx	2, 3	Rod element (solid mechanics) defined in R3.
Bx	2, 3	Beam element (solid mechanics) defined in R3.
Tx	3, 6	Triangular 2D element, defined in R2`or R:sup:`3.
Qx	4, 8, 9	Quadrilateral 2D element, defined in R2`or R:sup:`3.
TEx	4, 10	Tetrahedral element, defined in R3.
HE	8, 20, 27	Hexahedral element, defined in R3.
PRx	6, 15	Prismatic element, defined in R3.

Note that if an element is listed in the above table this does not necessarily mean that the corresponding element - for a given operator - is implemented in B2000++.

The field type contains the element class pertaining to the element geometry, augmented by the number of nodes. The extension field defines the actual element type, i.e. the operator, and can be chosen freely. Data set ELEMENT-PARAMETERS contains the element name translation table.

Wire, Line (L) and Rod/Cable (R) Elements

L (line), R (rod and cable) elements define line (wire) elements without any local y- and z-axis, i.e. the elements have axisymmetric properties around the local x-axis. L elements also constitute the basis for axisymmetric two-dimensional elements.

The element local x-axis is defined by the vector \(p_{21} = p_2 - p_1\), with \(p_1\) being the coordinate vector of the vertex \(n_1\) and \(p_2\) the coordinate vector of the vertex \(n_2\). The local y- and z-axes are not defined. Note that B2000++ node indices are positive integers (external numbering system) and they must belong to the same branch.

Rod and cable element to node connectivities.

Beam (B) Elements

Beam elements refer to the beam local orthogonal coordinate system, the local x-axis being tangential to the beam axis, adn the local y-axis and z-axis in a plane normal to the x-axis. The orientation of the local y- and z-axes are defined:

• by an orientation vector \(o\) defining the element local x-y plane with respect to the global coordinate system. The orientation vector must be specified by the MDL elements parameter beam_orientation.

• by a mesh node \(n_{ref}\) which defines the beam orientation vector \(o = n_{ref} - n_{1}\), where \(n_{1}\) is the coordinate vector of the first node defining the beam element. Note that the node identification is external, see nodes command.

The node identifiers \(n_i\) are positive integers and all node iidentifiers defining the element must belong to the same branch (mesh).

Beam element-to-node connectivities and element local orientation.

Unless analytical integration is performed the standard Gauss scheme is used, for B2 element a 1 point scheme and for B3 elements a 2 point scheme.

Triangular (T, TR) Elements

T, TR elements define triangular elements in R² and R³. B2000++ node identifiers \(n_i\) are positive integers and they must belong to the same branch. The element local x-axis x_element is defined by r₂₁ = p₂ - p₁, with p₂ being the coordinate of the vertex n₂, and p₁ the coordinate of the vertex n₁. The element local z-axis z_element is defined by the vector product r₂₁ . r₃₁, with r₃₁ = p₃ - p₁, and p₃ being the coordinate of the vertex n₃. The element local y-axis y_element is then obtained by the vector product z_element . x_element.

Element-to-node connectivities and element local orientations of triangular elements (left) and element edges (right).

T element edge connectivity

Edge	T3 element	T6 element
1	n1 n2	n1 n2 n4
2	n2 n3	n2 n3 n5
3	n3 n1	n3 n1 n6

All triangular elements requiring numerical integration have a built-in default integration rule. The default integration rule can be changed with the ischeme MDL element parameter.

Integration schemes

Element	Scheme	Description
T3	None	3 point standard triangle integration scheme.
T6	None	7 point standard triangle integration scheme.

Numerical integration scheme: Position and numbering of integration points.

Quadrilateral (Q) Elements

Q elements define quadrilateral elements in R² and R³. B2000++ node identifiers \(n_i\) are positive integers and they must belong to the same branch. The element local x-axis x_element is defined by r₂₁ = p₂ - p₁, with p₂ being the coordinate of the vertex n₂, and p₁ the coordinate of the vertex n₁. The element local z-axis z_element is defined by the vector product r₂₁ . r₃₁, with r₃₁ = p₃ - p₁, and p₃ being the coordinate of the vertex n₃. The element local y-axis y_element is then obtained by the vector product z_element .  x:_element.

Element-to-node connectivities and element local orientations of quadrilateral elements (left) and element edges (right).

Q element edge connectivity

Edge	Q4 element	Q8/Q9 element
1	n1 n2	n1 n2 n5
2	n2 n3	n2 n3 n6
3	n3 n4	n3 n4 n7
4	n4 n1	n4 n1 n8

Integration schemes

Element	Scheme	Description
Q4	None	3 point standard 2x2 Gauss integration scheme.
Q8, Q9	None	9 point standard 3x3 Gauss integration scheme.

Numerical integration scheme: Position and numbering of integration points.

Tetrahedral (TE) Elements

TE elements define tetrahedral elements in R³. B2000++ node identifiers \(n_i\) are positive integers and they must belong to the same branch. The element local x-axis x_element is defined by r₂₁ = p:sub:2 - p₁, with p₂ being the coordinate of the vertex n₂, and p₁ the coordinate of the vertex n₁. The element local z-axis z_element is defined by the vector product r₂₁ . r₃₁, with r₃₁ = p₃ - p₁, and p₃ being the coordinate of the vertex n₃. The element local y-axis y_element is then obtained by the vector product z_element .  x x_element.

Element-to-node connectivities and element local orientations of TE4 elements (left) and TE10 elements (right).

Element edges (left) and element faces (right).

Element face connectivity TE elements The element faces are numbered in counter-clockwise direction, as seen from outside the element. Thus, the element face normals (and the element face local z-axis) always point out from the element. The first 2 nodes of the element face connectivity list define the element face local x-axis x_face. The element face local y-axis is defined by y_face = r₂₁ . r₃₁, with r₂₁ = p₂ - p₁ and r₃₁ = p₃ - p₁, p₁ being the coordinate of the element face connectivity node 1, p₂ of node 2, and p₃ of node 3. The element face local y-axis y_face is then defined by z_face . x_face.

TE element face node connectivity

Face	TE4 faces	TE10 faces
1	n1 n3 n2	n1 n3 n2 n7 n6 n5
2	n1 n2 n4	n1 n2 n4 n5 n9 n8
3	n2 n3 n4	n2 n3 n4 n6 n10 n9
4	n3 n1 n4	n3 n1 n4 n7 n8 n10

Element edge connectivity TE elements The element edge node connectivity of TE elements are defined as follows: The first 2 nodes of an element edge connectivity list also define the element edge local x-axis x_edge, the axis running from the first to the second node. The figure and table below display the element local edge numbering, the orientation (direction) of the edge local x-axis, as well as the element nodes defining the edges.

TE element edge node connectivity

Edge	TE4	TE10
1	n1 n2	n1 n2 n5
2	n2 n3	n2 n3 n6
3	n3 n1	n3 n1 n7
4	n1 n4	n1 n4 n8
5	n2 n4	n2 n4 n9
6	n3 n4	n3 n4 n10

Integration schemes

Element	Scheme	Description
TE4	None	3 point standard 2x2 Gauss integration scheme.

Numerical integration scheme: Position and numbering of integration points.

Hexahedral (HE) Elements

HE elements define hexahedral elements in R³. B2000++ node identifiers \(n_i\) are positive integers and they must belong to the same branch. The element local x-axis x_element is defined by r₂₁ = p₂ - p₁, with p₂ being the coordinate of the vertex n₂, and p₁ the coordinate of the vertex n₁. The element local z-axis z_element is defined by the vector product r₂₁ . r₃₁, with r₃₁ = p₃ - p₁, and p₃ being the coordinate of the vertex n₃. The element local y-axis y_element is then obtained by the vector product z_element .  x x_element.

Element-to-node connectivities and element local orientations of HE elements. Left: HE8 and HE20. Right: HE27 additional nodes.

Element edges (left) and element faces (right).

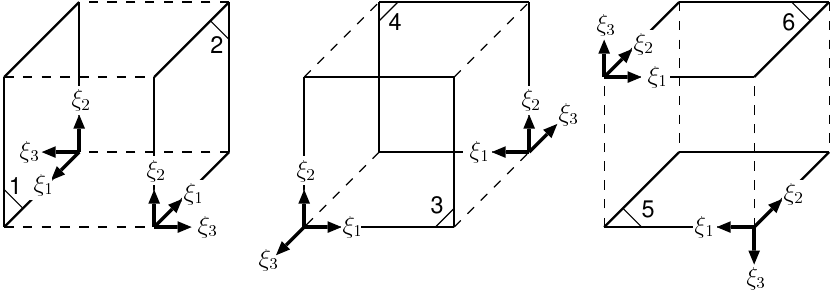
Element face local coordinate systems.

The element faces are numbered in counter-clockwise direction, as seen from outside the element. Thus, the element face normals (and the element face local z-axis) always point out from the element. The first 2 nodes of the element face connectivity list define the element face local x-axis x_face. The element face local y-axis is defined by y_face = r₂₁ . r₃₁, with r₂₁ = p₂ - p₁ and r₃₁ = p₃ - p₁, p₁ being the coordinate of the element face connectivity node 1, p₂ of node 2, and p₃ of node 3. The element face local y-axis y_face is then defined by z_face .  x x_face.

HE element face node connectivity

Face	HE8	HE20	HE27
1	n4 n1 n5 n8	n4 n1 n5 n8 n12 n17 n16 n20	n4 n1 n5 n8 n12 n17 n16 n20 n21
2	n2 n3 n7 n6	n2 n3 n7 n6 n10 n19 n14 n18	n2 n3 n7 n6 n10 n19 n14 n18 n22
3	n1 n2 n6 n5	n1 n2 n6 n5 n9 n18 n13 n17	n1 n2 n6 n5 n9 n18 n13 n17 n23
4	n3 n4 n8 n7	n3 n4 n8 n7 n11 n20 n1c5 n19	n3 n4 n8 n7 n11 n20 n15 n19 n24
5	n2 n1 n4 n3	n2 n1 n4 n3 n9 n12 n11 n10	n2 n1 n4 n3 n9 n12 n11 n10 n25
6	n5 n6 n7 n8	n5 n6 n7 n8 n13 n14 n15 n16	n5 n6 n7 n8 n13 n14 n15 n16 n26

Element edge connectivity HE elements The element edge node connectivity of HE elements are defined as follows: The first 2 nodes of an element edge connectivity list also define the element edge local x-axis x_edge, the axis running from the first to the second node. The figure and table below display the element local edge numbering, the orientation (direction) of the edge local x-axis, as well as the element nodes defining the edges.

HE element edge node connectivity

Edge	HE8	HE20/HE27
1	n1 n2	n1 n2 n9
2	n2 n3	n2 n3 n10
3	n3 n4	n3 n4 n11
4	n4 n1	n4 n1 n12
5	n5 n6	n5 n6 n13
6	n6 n7	n6 n7 n14
7	n7 n8	n7 n8 n15
8	n8 n5	n8 n5 n16
9	n1 n5	n1 n5 n17
10	n2 n6	n2 n6 n18
11	n3 n7	n3 n7 n19
12	n4 n8	n4 n8 n20

Numerical integration scheme: Position and numbering of integration points.

Prismatic (PR) Elements

PR elements define prismatic elements in R³. B2000++ node identifiers \(n_i\) are positive integers and they must belong to the same branch. The element local x-axis x_element is defined by r₂₁ = p₂ - p₁, with p₂ being the coordinate of the vertex n₂, and p₁ the coordinate of the vertex n₁. The element local z-axis z_element is defined by the vector product r₂₁ . r₃₁, with r₃₁ = p₃ - p₁, and p₃ being the coordinate of the vertex n₃. The element local y-axis y_element is then obtained by the vector product z_element . x x_element.

Element-to-node connectivities and element local orientations of PR elements.

Element face connectivity PR elements The element faces are numbered in counter-clockwise direction, as seen from outside the element. Thus, the element face normals (and the element face local z-axis) always point out from the element. The first 2 nodes of the element face connectivity list define the element face local x-axis x_face. The element face local y-axis is defined by y_face = r₂₁ . r₃₁, with r₂₁ = p₂ - p₁ and r₃₁ = p₃ - p₁, p₁ being the coordinate of the element face connectivity node 1, p₂ of node 2, and p₃ of node 3. The element face local y-axis y_face is then defined by z_face . x x_face.

PR element face node connectivity

1	n1 n3 n2	n1 n3 n2 n9 n8 n7
2	n4 n5 n6	n4 n5 n6 n10 n11 n12
3	n1 n2 n5 n4	n1 n2 n5 n4 n7 n14 n10 n13
4	n2 n3 n6 n5	n2 n3 n6 n5 n8 n15 n11 n14
5	n3 n1 n4 n6	n3 n1 n4 n6 n9 n13 n12 n15

Element edge connectivity PR elements The element edge node connectivity of PR elements are defined as follows: The first 2 nodes of an element edge connectivity list also define the element edge local x-axis x_edge, the axis running from the first to the second node. The figure and table below display the element local edge numbering, the orientation (direction) of the edge local x-axis, as well as the element nodes defining the edges.

PR element edge node connectivity

Edge	PR6	PR15
1	n1 n2	n1 n2 n7
2	n2 n3	n2 n3 n8
3	n3 n1	n3 n1 n9
4	n4 n5	n4 n5 n10
5	n5 n6	n5 n6 n11
6	n6 n4	n6 n4 n12
7	n1 n4	n1 n4 n13
8	n2 n5	n2 n5 n14
Edge 9:	n3 n6	n3 n6 n15

Point Mass (PMASS) Element

The PMASS element adds mass at a given grid point with respect to the element-local axes. Note that B2000++ node identifiers \(n_i\) are positive integers and they must belong to the same branch.

Point mass element connectivity and local coordinate system.

Rigid Body (RBE) Elements

The RBE element connects a master node to one or several slave nodes.