B2000++ Materials

This part describes the materials models of B2000+++ and how to define material properties with the material command of MDL. Currently the following materials are supported:

Solid mechanics materials
Heat flow materials
User defined materials (requires user-written material code).

Solid Mechanics Materials

This part describes the materials models of B2000+++ and how to define material properties with the material command of MDL.

Solid mechanics material overview
Material type	Description
isotropic	Linear elastic and isotropic material models for stress analysis.
orthotropic	Linear elastic and orthotropic material models for stress analysis.
laminate, abd, pshell	Laminates and equivalent-stiffness-layer material models for stress analysis.
viscoelastic	Viscoelastic linear materials models for stress analysis.
heat	Linear and nonlinear material models for heat analysis.
user	User-defined material.

Linear elastic materials models are supported by all stress elements (rod/cable, beam, 2D, shell, and 3D elements). Isotropic, orthotropic, and anisotropic material properties can be specified.

Linear Elastic Isotropic Material

Linear elastic isotropic materials are supported by all stress elements (rod/cable, beam, 2D, shell, and 3D elements).

MDL Material Specification

material id type isotropic
  E <float>
  [nu <float>]
  [alpha <float>]
  [failure ... end]
  [density <float>]
end

MDL Parameters

E <float>: Specifies the modulus of elasticity E.
nu <float>: Specifies Poisson’s ratio nu. Default is 0.
alpha <float>: Specifies the thermal expansion coefficient. Default is 0.
failure ... end: Specifies a Solid Mechanics Failure Criteria criterion (optional).
density <float>: Specifies the material density. Default is 0.

Linear Elastic Orthotropic Material

Linear elastic orthotropic material models are supported by all 2D, shell, and 3D stress elements). Depending on the element, not all material constants need to be specified.

MDL Material Specification

material id type orthotropic
  [planestrain]
  E1 <float> E2 <float> E3 <float>
  nu12 <float> nu13 <float> nu23 <float>
  g12 <float> g13 <float> g23 <float>
  [alpha11 <float> alpha22 <float> alpha33 <float> alpha12 <float> alpha13 <float> alpha23 <float>]
  [failure ... end]
  [density <float>]
end

MDL Parameters

E1 <float> E2 <float> E3 <float>: Specifies the moduli of elasticity in the material directions 1, 2, and 3. All 3 constants are required.
planestrain: Specifies plane-strain elasticity. For 2D elements, default is plane-stress. Is ignored by non-2D elements (shell elements are always plane-stress, and 3D elements are neither plane-strain nor plane-stress).
nu12 <float> nu13 <float> nu23 <float>: Specifies Poisson’s ratio relating the different material directions. Shell elements and 2D elements make use of nu13 and nu23 for the plane-stress and plane-strain (2D elements only) conditions, respectively. All 3 constants are required.
g12 <float> g13 <float> g23 <float>: Specifies the shear modulus. 2D elements will ignore g13 and g23. All 3 constants are required.
alpha11 <float> alpha22 <float> alpha33 <float> alpha12 <float> alpha13 <float> alpha23 <float>: Specifies the thermal expansion coefficients. Default is 0. 2D elements will ignore alpha33|alpha13|alpha23.

failure ... end

Specifies a Solid Mechanics Failure Criteria (optional).

density <float>: Specifies the material density density. Default is 0.

Example:

material 1 type orthotropic
  e1 124000.0
  e2 9000.0
  nu12 0.3
  g12 5100.0
  g13 5100.0
  g23 5000.0
  density 1.53e3
end

Orthotropic strain-stress relation

The strain-stress (compliance) relation of a linear elastic orthotropic 3D material is defined as follows:

\[\begin{split}\begin{Bmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{33} \\ \gamma_{12} \\ \gamma_{23} \\ \gamma_{13} \\ \end{Bmatrix} = \begin{pmatrix} \frac{1}{E_{1}} & {- \frac{\nu_{12}}{E_{1}}} & {- \frac{\nu_{13}}{E_{1}}} & 0 & 0 & 0 \\ & \frac{1}{E_{2}} & {- \frac{\nu_{23}}{E_{2}}} & 0 & 0 & 0 \\ & & \frac{1}{E_{3}} & 0 & 0 & 0 \\ & & & \frac{1}{G_{12}} & 0 & 0 \\ & & & & \frac{1}{G_{23}} & 0 \\ {symm} & & & & & \frac{1}{G_{13}} \\ \end{pmatrix}\begin{Bmatrix} \sigma_{11} \\ \sigma_{22} \\ \sigma_{33} \\ \tau_{12} \\ \tau_{23} \\ \tau_{13} \\ \end{Bmatrix}\end{split}\]

The strain-stress (compliance) relation of a linear elastic orthotropic 2D material is defined as follows:

\[\begin{split}\begin{Bmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \gamma_{12} \\ \end{Bmatrix} = {\begin{pmatrix} \frac{1}{E_{1}} & {- \frac{\nu_{12}}{E_{1}}} & 0 \\ & \frac{1}{E_{2}} & 0 \\ {symm} & & \frac{1}{G_{12}} \\ \end{pmatrix}\begin{Bmatrix} \sigma_{11} \\ \sigma_{22} \\ \tau_{12} \\ \end{Bmatrix}}\text{,}\begin{Bmatrix} \varepsilon_{11} \\ \varepsilon_{22} \\ \gamma_{12} \\ \end{Bmatrix} = {\begin{pmatrix} \frac{1 - \nu_{12}^{2}}{E_{1}} & \frac{\nu_{12}\left( \nu_{12} - 1 \right)}{E_{1}} & 0 \\ & \frac{1 - \nu_{12}^{2}}{E_{2}} & 0 \\ {symm} & & \frac{1}{G_{12}} \\ \end{pmatrix}\begin{Bmatrix} \sigma_{11} \\ \sigma_{22} \\ \tau_{12} \\ \end{Bmatrix}}\end{split}\]

Linear Elastic ortho25 Material

The “ortho25” (two-and-a-half dimensions) material is applied to laminates, where the shear in the element normal direction has to be taken into account.

MDL Material Specification

  material id type ortho25
    e1 <float> e2 <float>
    nu12 <float> nu13 <float> nu23 <float>
    g12 <float> g13 <float> g23 <float>
    [alpha11 <float> alpha22 <float>]
    [failure ... end]
    [density <float>]
  end
mid 6 # m1
 type ortho25
 e1 1.473000e+05 e2 1.180000e+04
 p1 3.000000e-01
 g1 6.000000e+03 g2 3770 g3 6000

MDL Parameters

E1 <float> E2 <float>: Specifies the moduli of elasticity in the material directions 1 and 2. Required.
nu12 <float>: Specifies Poisson’s ratio in-plane. Required.
g12 <float> g13 <float> g23 <float>: Specifies the shear moduli. All 3 constants are required.
alpha11 <float> alpha22 <float>: Specifies the thermal expansion coefficients. Optional.

failure ... end

Specifies a Solid Mechanics Failure Criteria (optional).

density <float>: Specifies the material density density. Default is 0.

Example

Laminate material definition from verification case psc5.

material 1
    type ortho25
    e1 1.473000e+05 e2 1.180000e+04
    p1 3.000000e-01
    g1 6.000000e+03 g2 3770 g3 6000
end

Hyperelastic materials models are provided with B2000++ Pro and are supported by 2D and 3D elements.

Linear Elastic Anisotropic Material

Linear elastic anisotropic material models are supported by all shell and 3D stress elements.

MDL Material Specification

material id type anisotropic
  [planestrain]
  c1111|c1122|c1133|c1112|c1113|c1123|
        c2222|c2233|c2212|c2213|c2223|
              c3333|c3312|c3313|c3323|
                    c1212|c1213|c1223|
                          c1313|c1323|
                                c2323|
  [alpha11 <float> alpha22 <float> alpha33 <float> alpha12 <float> alpha13 <float> alpha23 <float>]
  [failure ... end]
  [density  <float>]
end

MDL Parameters

planestrain: Specifies plane-strain elasticity. For 2D elements, default is plane-stress. Is ignored by non-2D elements (shell elements are always plane-stress, and 3D elements are neither plane-strain nor plane-stress).
cijkl <float>: Specifies an entry in the constitutive matrix. Default is 0 for all entries.
alpha11 <float> alpha22 <float> alpha33 <float> alpha12 <float> alpha13 <float> alpha23 <float>: Specifies the thermal expansion coefficients. Default is 0. 2D elements will ignore alpha33|alpha13|alpha23.

failure ... end

Specifies a Solid Mechanics Failure Criteria criterion (optional).

density <float>: Specifies the material density density. Default is 0.

Laminates

Laminates are supported by shell elements and by hexahedral and prismatic 3D elements.

MDL Material Specification

material id type laminate
  t al id
  t al id
  ...
end

The plies of the laminate are arranged in the element thickness direction from the bottom surface to the top surface, with the first ply located at the bottom and the last ply located at the top. Each ply must specify the ply thickness t, the angle of rotation al (in degrees), and the material identifier id of the layer. The angle of rotation is specified around the element surface, according to the right-hand rule (see figure below).

_images/laminate-el-coor.svg — Element and laminate coordinate system orientation (Q elements).

_images/laminate-stack.svg — Laminate in stack orientation.

Note

See additional information in the Special Topics Section Laminates.

ABD Material

The ABD material model is a linear equivalent-stiffness-layer material model for shell analysis with the plane stress assumption. It allows to directly specify the A,B,D matrices from classical laminate theory. It is supported by all shell elements.

MDL Material Specification

material id type abd
  membrane_matrix [ <C1111> <C1122> <C1112> <C2222> <C2212> <C1212> ]
  bending_matrix [ <C1111> <C1122> <C111>2 C2222> <C2212> C1212> ]
  coupling_matrix [ <C111>1 <C1122> <C1112> <C2222> <C2212> <C1212> ]
  transverse_shear_matrix [ <C1313> <C2313> <C2323> ]
  membrane_alpha [<A11> <A22> <A12>]
  bending_alpha [<A11> <A22> <A12>]
  mass <float>
end

membrane_matrix [ <C1111> <C1122> <C1112> <C2222> <C2212> <C1212> ]

Specifies the components Cijkl of the upper part of the symmetric 3x3 matrix of the membrane shell section stiffness. It corresponds to the A-matrix of classical laminate theory.

bending_matrix[ <C1111> <C1122> <C111>2 C2222> <C2212> C1212> ]: Specifies the upper part of the symmetric 3x3 matrix of the bending shell section stiffness. It corresponds to the D-matrix of classical laminate theory.
coupling_matrix[ <C111>1 <C1122> <C1112> <C2222> <C2212> <C1212> ]: Specifies the upper part of the symmetric 3x3 membrane-bending coupling matrix. It corresponds to the B-matrix of classical laminate theory.
transverse_shear_matrix [ <C1313> <C2313> <C2323> ]: Specifies the upper part of the symmetric 2x2 matrix containing the transverse-shear shell section stiffnesses. It is required by shear-deformable shell elements such as the MITC elements. This matrix must incorporate the shear correction factor. For example, with isotropic materials, the two diagonal elements would have a value of \(\frac{5}{6}\frac{Et}{2(1+\nu)}\) where \(t\) is the shell thickness, \(E\) the modulus of elasticity, and \(\nu\) Poisson’s ratio.
membrane_alpha [<A11> <A22> <A12>]: Specifies the thermal expansion coefficients for the membrane components of the strain tensor.
bending_alpha [<A11> <A22> <A12>]: Specifies the thermal expansion coefficients for the bending components of the strain tensor.
mass <float>: Specifies the mass per unit area.

All shell elements are assumed to have a thickness of 1 and an eccentricity of 0, regardless of what is specified otherwise. Hence, the matrices are not scaled by a thickness, instead, they are utilized as is specified.

The material law is as follows:

\[\begin{split}\begin{bmatrix} \sigma^{m} \\ \sigma^{b} \\ \sigma^{s} \\ \end{bmatrix} = \begin{bmatrix} A & B & 0 \\ B^{T} & D & 0 \\ 0 & 0 & S \\ \end{bmatrix}\left( \begin{bmatrix} \varepsilon_{m} \\ \varepsilon_{b} \\ \varepsilon_{s} \\ \end{bmatrix} - {\Delta T}\begin{bmatrix} \alpha_{m} \\ \alpha_{b} \\ 0 \\ \end{bmatrix} \right)\end{split}\]

where \(\Delta T\) is the difference between the interpolated temperature to the reference temperature (see the MDL temperatures command). It is evaluated at the shell mid-surface (it is the average of the values at the bottom and top shell surface).

The in-layer strains and stresses are not calculated and are not written to the database. Instead, the shell section strains, expressed in the material reference frame, are stored in the STRAIN_SHELL_MATERIAL dataset, with the components aligned with the ABD material matrix. The shell section stresses, also expressed in the material reference frame, are stored in the STRESS_SHELL_MATERIAL dataset Field.

PSHELL Material

The PSHELL material model is a linear equivalent-stiffness-layer material model for shell analysis with the plane stress assumption. It is supported by all shell elements. Its purpose is to provide compatibility with FE models that were created for Nastran.

MDL Material Specification

material id type pshell
  [membrane_mid mid]
  [bending_mid mid]
  [tranverse_shear_mid mid]
  [coupling_mid mid]
  [bending_scale_factor f]
  [shear_correction_factorvf]
  [thickness t]
  [non_structural_mass m]
end

The MITC elements are Reissner-Mindlin shell elements and as such require a nonzero but finite transverse-shear stiffness. The B2000++ implementation of PSHELL ensures this: If no material id for the transverse shear is given, transverse-shear stiffness will be derived from the membrane material. If no membrane material is specified, transverse-shear stiffness will be derived from the bending material.

According to Nastran conventions, the transverse shear stiffness is extracted as follows according to the type of material: For isotropic materials, g is used. For orthotropic materials, g13 and g23 are used. For anisotropic materials, the sub-matrix [[C1111,C1122],[C1122,C2222]] is used.

If no thickness is specified for the PSHELL material, a thickness for the shell element must be specified. The thickness is used to scale the membrane matrix and the transverse shear stiffnesses by \(t\) and the bending matrix by \(\frac{t^{3}}{12}\). The coupling matrix is not scaled.

To account for non-homogeneous materials, the bending_scale_factor (default 1) can be modified.

The shear_correction_factor (default 5/6) should not be set to zero.

Mooney-Rivlin Material Model

The nonlinear hyperelastic Mooney-Rivlin material model is suited for finite strain analysis of rubber-like isotropic materials. The elastic potential includes a hydrostatic work term. This material model is supported by 2D and 3D elements.

MDL Material Specification

material id type mooney_rivlin
   c1 <float>
   [c2 <float>]
   kappa <float>
   [alpha <float>]
   [failure ... end]
   [density <float>]
end

MDL Parameters

c1|c2 <float>: Specifies the Mooney-Rivlin material constants. If c2 is not specified, it will be assumed 0, in which case a Neo-Hookean material is described.
kappa <float>: Specifies the bulk modulus.
alpha <float>: Specifies the thermal expansion coefficient. Default is 0.

failure ... end

Specifies a Solid Mechanics Failure Criteria criterion (optional).

density <float>: Specifies the material density. Default is 0.

Alternatively, the elastic modulus e and Poisson’s ratio nu may be specified instead of the Mooney-Rivlin coefficients c1, c2, and kappa. In this case, the Mooney-Rivlin material constants will be calculated from e and nu.

Generalised Blatz-Ko Material Model

The nonlinear hyperelastic generalized Blatz-Ko material model is suited for finite strain analysis of foam-rubber materials. The elastic potential includes a hydrostatic work term. This material model is supported by 3D elements.

MDL Material Specification

material id type blatz_ko
   g <float>
   nu <float>
   [f <float>]
   [alpha <float>]
   [failure ... end]
   [density <float>]
end

MDL Parameters

g <float>

Specifies the shear modulus.

nu <float>

Specifies Poisson’s ratio.

f <float>

Specifies the volume-fraction of voids in the foam-rubber material. Default is 0.5.

alpha <float>: Specifies the thermal expansion coefficient. Default is 0.

failure

Specifies a Solid Mechanics Failure Criteria criterion (optional).

density <float>

Specifies the material density. Default is 0.

Alternatively, the elastic modulus e may be specified instead of the shear modulus g.

Viscoelastic Isotropic Material

The visco-elastic material models is an elastic isotropic material with dynamic material damping properties according to the Generalized Maxwell Model (GMM):

_images/maxwell-material-model.svg — Schematic representation of Maxwell model

Visco-elastic material models are supported by shell and 3D elements and assume small strains.

MDL Material Specification

material id type viscoelastic_isotropic
  e <float>
  nu <float>
  g <float>
  relative_moduli flist
  relaxation_times flist
  [volumetric yes|no]
  [instantaneous_elasticity yes|no]
  [alpha <float>]
  [density <float>]
end

MDL Parameters

e <float>: Specifies the modulus of elasticity.
nu <float>: Specifies Poisson’s ratio. Default is 0.
relative_moduli flist: Specifies the values of the relative moduli of the GMM elements. The number of values must be identical to those in relaxation_times.
relaxation_times flist: Specifies the relaxation times for the GMM elements. The number of values must be identical to those in relative_moduli.
volumetric yes|no: Specifies if the components refer to volumetric tensor or not. Default is yes. If no is specified, the volumetric-deviatoric split is performed, and the viscous damping is performed only on the deviatoric components.
instantaneous_elasticity yes|no: Specifies if the relaxation function assumes instantaneous elasticity. Default is yes (creep). If no is specified, viscous damping is performed.
alpha <float>: Specifies the thermal expansion coefficient. Default is 0.

failure ... end

Specifies a Solid Mechanics Failure Criteria criterion (optional).

density <float>: Specifies the material density. Default is 0.

Viscoelastic Orthotropic Material

The visco-elastic orthotropic material model is an elastic orthotropic material with dynamic material damping properties according to the Generalized Maxwell Model (GMM) (see Schematic representation of Maxwell model) and it is supported by shell and 3D elements and assumes small strains.

MDL Material Specification

material id type viscoelastic_orthotropic
  e1|e2|e3 <float>
  nu12|nu13|nu23 <float>
  g12|g13|g23 <float>
  relative_moduli_ij flist
  relaxation_times_ij flist
  [volumetric yes|no]
  [instantaneous_elasticity yes|no]
  [alpha11|alpha22|alpha33|alpha12|alpha13|alpha23 <float>]
  [density <float>]
end

MDL Parameters

e1|e2|e3 <float>: Specifies the modulus of elasticity in the material directions. If e is specified
nu12|nu13|nu23 <float>: Specifies Poisson’s ratio relating the different material directions. Shell elements make use of nu13 and nu23 for the plane-stress condition.
g12|g13|g23 <float>: Specifies the shear modulus.
relative_moduli_ij flist: Specifies the values of the relative moduli of the GMM elements in the material direction ij (11, 22, 33, 12, 13, 23). The number of values must be identical to those in relaxation_times.
relaxation_times_ij flist: Specifies the relaxation times for the GMM elements in the material direction ij (11, 22, 33, 12, 13, 23). The number of values must be identical to those in relative_moduli_ij.
volumetric yes|no: Specifies if the components refer to volumetric tensor or not. Default is yes. If no is specified, the volumetric-deviatoric split is performed, and the viscous damping is performed only on the deviatoric components.
instantaneous_elasticity yes|no: Specifies if the relaxation function assumes instantaneous elasticity. Default is yes (creep). If no is specified, viscous damping is performed.
alpha11|alpha22|alpha33|alpha12|alpha13|alpha23 <float>: Specifies the thermal expansion coefficients. Default is 0.

failure ... end

Specifies a Solid Mechanics Failure Criteria criterion (optional).

density <float>: Specifies the material density. Default is 0.

Theoretical Background

The convolution integral of the constitutive equation of a generalized Maxwell element for a linear initial material and infinitesimal (‘small’) strain is

\[{\sigma_{ij}\left( t \right)} = {\int\limits_{u = {- \infty}}^{t}{{{g_{ij}\left( {t - u} \right)}{\overset{.}{\sigma}}_{ij}^{0}}{du}}}\]

and the normalized relaxation functions are defined as

\[{g_{ij}\left( t \right)} = {\gamma_{ij}^{\infty} + {\sum\limits_{\operatorname{k=}1}^{N}{\gamma_{ij}^{k}e^{\frac{-t}{\tau_{i}}}}}}\]

\[\gamma_{ij}^{\infty} = {1 - {\sum\limits_{k = 1}^{N}\gamma_{ij}^{k}}}\]

\(\tau_{i}\) is the relaxation time and \(\gamma_{i}\) the relative modulus of the i^th out of \(N\) Maxwell elements.

This model is sometimes extended with an additive split of the strain as a deviatoric and a volumetric strain with a different constitutive equation for each part of the strain (option volumetric no). This is justified for nearly incompressible materials like some polymeric materials where the bulk response is only elastic and the deviatoric response is viscoelastic. The material model assumes ‘small’ strains, which is justified for metallic or composite materials.

The relaxation function as reported above assumes instantaneous elasticity. If not (parameter instantaneous_elasticity set to no), then the relaxation function g is defined as:

\[{g_{ij}\left( t \right)} = {1 + {\sum\limits_{i = 1}^{N}{\gamma_{ij}^{k}e^{\frac{-t}{\tau_{i}}}}}}\]

Staverman and Schwarz [Staverman52] gave the expression of the free energy for a generalized Maxwell element in one dimension. Piero and Deseri [Piero96] generalized this expression to three-dimensional linear viscoelasticity. The free energy \(F\) of the generalized Maxwell element is

\[F = {\iint\limits_{{u,v} = {- \infty}}^{t}{{g\left( {{2t} - {u - v}} \right)}{\overset{.}{\varepsilon}\left( u \right)}C^{0}\overset{.}{\varepsilon}{{\left( v \right)}{{du}{dv}}}}}\]

Using the thermodynamic equation

\[{\sigma\overset{.}{\varepsilon}} = {F + {T_{0}\Theta}}\]

\(T_{0}\) is the constant temperature and \(\Theta\) the entropy production. By differentiating with respect to the time we obtain the rate of dissipated energy \(D = {T_{0}\Theta}\)

\[D = {- \iint\limits_{{u,v} = {- \infty}}^{t}}\]

Solid Mechanics Failure Criteria

Failure indices are evaluated on a per element base whenever the element material refers to on of the failure criteria described in this section.

Maximum Principal Stress Failure Criterion

With the maximum pricipal stress \(\sigma_i\) failure criterion failure is said to occur if

\[\begin{split}\sigma_1 >= t \quad | \quad \sigma_3 <= c \quad \quad \quad in R^{3} \\ \sigma_1 >= t \quad | \quad \sigma_2 <= c \quad \quad \quad in R^{2}\end{split}\]

The maximum principal stress failure criterion (Rankine) is intended for brittle materials. In plane stress Failure will occur if

MDL Failure Criterion Specification within Material Block

failure max_principal_stress
    t <float>
    c <float>
    s <float>
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

t <float>: Specifies the maximum tensile yield stress, that is, the maximum value of the largest of the 3 principal stresses.
c <float>: Specifies the maximum compressive yield stress, that is, the minimum value of the smallest of the 3 principal stresses.
s <float>: Specifies the maximum shear stress.
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float>: Specifies the minimum failure index which is required to store the evaluated failure criterion in the database (B2000++). Default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_MAX_PRINCIPAL_STRESS dataset. For each element integration point, the maximum failure index, the corresponding margin-of-safety, the number of the failure mode (“component”) are stored, and the failure indices for the tensile, compressive, and shear stresses are stored. The convention is such that a failure mode of 1 corresponds to the tensile stress, a failure mode of 2 corresponds to the compressive stress, and a failure mode of 3 to the shear stress.

Example

material 1 type isotropic
  # Aluminium 2024-T3
  e     72400.     # [MPa]
  nu        0.33
  density   2.8e-9 # [t/mm^3]
  alpha    22.8e-6 # [1/K]
  failure max_principal_stress
    t 138.0 # [MPa]
    c 138.0 # [MPa]
    s 138.0 # [MPa]
  end
end

Maximum Stress Failure Criterion

A linear criterion based on tension, compression and shear stress. Failure occurs when

\[t <= \sigma_{11} <= c \quad | \quad t <= \sigma_{22} <= c \quad | \quad \sigma_{12} >= s\]

MDL Failure Criterion Specification within Material Block

failure max_stress
    t <float> (t1 <float> t2 <float> t3 <float>)
    c <float> (c1 <float> c2 <float> c3 <float>)
    s <float> (s12 <float> s23 <float> s13 <float>)
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

t <float> (t1 <float> t2 <float> t3 <float>): Specifies the value of the tension failure stresses. t1 is defined in the material direction 1, t2 in the material direction 2, and t3 in the material direction 3. Except for plane-stress conditions, where t3 can be omitted, all parameters must be specified and positive. Specification of t implies t1 t2 t3 t.
c <float> (c1 <float> c2 <float> c3 <float>): Specifies the value of the compressive failure stresses. c1 is defined in the material direction 1, c2 in the material direction 2, and c3 in the material direction 3. Except for plane-stress conditions, where c3 can be omitted, all parameters must be specified and positive. Specification of c implies c1 c2 c3 c.
s <float> (s12 <float> s23 <float> s13 <float>: Specifies the value of the shear failure stresses. Except for plane-stress conditions, where s23 and s13 can be omitted, all parameters must be specified and positive. Specification of s implies s12 s23 s13 s.
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float>: Specifies the minimum failure index which is required to store the evaluated failure criterion in the database (B2000++). Default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_MAX_STRESS dataset. For each element integration point, the maximum failure index, the corresponding margin-of-safety, and the number of the failure mode (“component”) are stored. Note that the components of the stress tensor must be arranged in the sequence

[Sxx, Syy, Szz, Sxy, Syz, Sxz]

and that a failure mode of 1 corresponds to the first stress component, a failure mode of 2 corresponds to the second stress component, etc.

Example:

material 1 type isotropic
  # Aluminium 2024-T3
  e 72400.     # [MPa]
  nu 0.33
  density 2.8e-9 # [t/mm^3]
  alpha 22.8e-6 # [1/K]
  failure max_stress
    t 138.0 # [MPa]
    c 138.0 # [MPa]
    s 138.0 # [MPa]
  end
end

Maximum Principal Strain Failure Criterion

With the maximum pricipal strain \(\epsilon_i\) failure criterion failure is said to occur if

\[\begin{split}\epsilon_1 >= t \quad | \quad \epsilon_3 <= c \quad \quad \quad in R^{3} \\ \epsilon_1 >= t \quad | \quad \epsilon_2 <= c \quad \quad \quad in R^{2}\end{split}\]

MDL Failure Criterion Specification within Material Block

failure max_principal_strain
    t <float>
    c <float>
    s <float>
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

t: Specifies the maximum tensile strain, that is, the maximum value of the largest of the 3 principal strains.
c <float>: Specifies the maximum compressive strain, that is, the minimum value of the smallest of the 3 principal strains.
s <float>: Specifies the maximum shear strain.
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float> Specifies the minimum failure index which is required to: store the evaluated failure criterion in the database. The default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_MAX_PRINCIPAL_STRAIN dataset. For each element integration point, the maximum failure index, the corresponding margin-of-safety, the number of the failure mode (“component”) are stored, and the failure indices for the tensile, compressive, and shear strains are stored. The convention is such that a failure mode of 1 corresponds to the tensile strain, a failure mode of 2 corresponds to the compressive strain, and a failure mode of 3 to the shear strain.

Example:

material 1 type isotropic
  # Aluminium 2024-T3
  E 72400.     # [MPa]
  nu 0.33
  density 2.8e-9 # [t/mm^3]
  alpha 22.8e-6 # [1/K]
  failure max_principal_strain
    t +4500.e-6
    c -3000.e-6
    s +5000.e-6
    filter max_of_element
  end
end

Maximum Strain Failure Criterion

A linear criterion based on tension, compression and shear strain. Failure occurs when

\[t_i <= \epsilon_{ii} <= c_i \quad | \quad \epsilon_{ij} >= s_ij\]

MDL Failure Criterion Specification within Material Block

failure max_principal_strain
    t|t1|t2|t3 <float>
    c|c1|c2|c3 <float>
    s|s12|s23|s13 <float>
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

t|t1|t2|t3 <float>: Specifies the value of the tension failure strains. t1 is defined in the material direction 1, t2 in the material direction 2, and t3 in the material direction 3. Except for plane-strain conditions, where t3 can be omitted, all parameters must be specified and positive. Specification of t implies t1=t2=t3=t.
c|c1|c2|c3 <float>: Specifies the value of the compressive failure strains. c1 is defined in the material direction 1, c2 in the material direction 2, and c3 in the material direction 3. Except for plane-strain conditions, where c3 can be omitted, all parameters must be specified and positive. Specification of c implies c1=c2=c3=c.
s|s12|s23|s13 <float>: Specifies the value of the shear failure strains. Except for plane-strain conditions, where s23 and s13 can be omitted, all parameters must be specified and positive. Specification of s implies s12=s23=s13=s. The shear strengths should be given as true strains (not as engineering strains, that is, not multiplied by 2).
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float> Specifies the minimum failure index which is required to: store the evaluated failure criterion in the database. The default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_MAX_STRAIN dataset. For each element integration point, the maximum failure index, the corresponding margin-of-safety, and the number of the failure mode (“component”) are stored.

Von Mises Failure Criterion

Specifies the von Mises failure criterion for the current material.

MDL Failure Criterion Specification within Material Block

failure von_mises
    r <float>
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

r <float>: Specifies the von Mises equivalent stress strength value for the (isotropic) strength for tension, compressive, and shear. This parameter is required and must be positive. Setting``r`` to 1.0 will produce the von Mise sequivalent stress instead.
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float>: Specifies the minimum failure index which is required to store the evaluated failure criterion in the database. The default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_VON_MISES dataset. For each element integration point, the maximum failure index and the corresponding margin-of-safety are stored.

Tsai-Wu Failure Criterion

Specifies the Tsai-Wu failure criterion for the current material.

MDL Failure Criterion Specification within Material Block

failure tsai_wu
    t|t1|t2|t3 <float>
    c|c1|c2|c3 <float>
    s|s12|s23|s13 <float>
    f12i <float>
    f13i <float>
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

t|t1|t2|t3 <float>: Specifies the value of the tension failure stresses. t1 is defined in the material direction 1, t2 in the material direction 2, and t3 in the material direction 3. Except for plane-stress conditions, where t3 can be omitted, all parameters must be specified and positive. Specification of t implies t1=t2=t3=t.
c|c1|c2|c3 <float>: Specifies the value of the compressive failure stresses. c1 is defined in the material direction 1, c2 in the material direction 2, and c3 in the material direction 3. Except for plane-stress conditions, where c3 can be omitted, all parameters must be specified and positive. Specification of c implies c1=c2=c3=c.
s|s12|s23|s13 <float>: Specifies the value of the shear failure stresses. Except for plane-stress conditions, where s23 and s13 can be omitted, all parameters must be specified and positive. Specification of s implies s12=s23=s13=s.
f12i|f23i <float>: Specifies the Tsai-Wu interaction coefficients (in the range of [-1, 1)].
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float>: Specifies the minimum failure index which is required to store the evaluated failure criterion in the database. The default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_TSAI_WU dataset. For each element integration point, the maximum failure index and the corresponding margin-of-safety are stored.

Hashin Failure Criterion

Specifies the [Hashin80] failure criterion for the current material. This failure criterion is intended for transversely isotropic materials. For a consistent response when \(\sigma_{11}\) is almost zero, the shear stresses \(\tau_{12}\) and \(\tau_{23}\) are not used to detect fiber tensile failure, that is, \({fi1+} = \frac{\sigma_{11}}{t1}\).

MDL Failure Criterion Specification within Material Block

failure max_principal_stress
    t <float>
    c <float>
    s <float>
    filter max_of_element
    fi_min <float>
end

MDL Failure Criterion Parameters

inplane yes|no: If set to yes, assume a plane stress state and use the plane stress failure criterion rather than the 3D failure criterion which is the default.
t1 <float>: The axial tensile failure stress.
c1 <float>: The axial compressive failure stress.
t2 <float>: The transverse tensile failure stress.
c2 <float>: The transverse compressive failure stress.
s12 <float>: The axial shear failure stress.

s23 <float>

The transverse shear failure stress. If not available from material data, it can be obtained, assuming pure compressive and an angle of 53 degrees for the fracture surface, using equation 68: \({s23} = 0.378*{c2}\), see [Larc04].

filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float>: Specifies the minimum failure index which is required to store the evaluated failure criterion in the database. The default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX dataset, the values of the failure criterion evaluated at the element integration points are stored in the FC_HASHIN dataset. For each element integration point, the maximum failure index, the corresponding margin-of-safety, and the number of the failure mode (“component”) are stored: 1 means fiber tensile, 2 fiber compressive, 3 matrix tensile, and 4 means matrix compressive.

Example:

material 1 type orthotropic
  # T300/1034-C graphite/epoxy, units in [MPa]
  e1 146.86e+03
  e2 11.376e+03
  e3 11.376e+03
  nu12 0.3
  nu13 0.3
  nu23 0.3
  g1 6.186e+03
  g2 6.186e+03
  g3 6.186e+03

  failure hashin
    t1  1730.0
    t2    66.5
    c1  1379.0
    c2   268.2
    s12  133.763
    s23  101.4
  end
end

LaRC04 Failure Criterion

Specifies the LaRC04 failure criterion for the current material. It is implemented as a plane stress failure criterion according to Maimi et.al [mcmd06], rather than according to the original LaRC04 description [Larc04], which describes a 3D failure criterion.

MDL Failure Criterion Specification within Material Block

failure larc04
    parameters
end

MDL Failure Criterion Parameters

t1|t2 <float>: Specifies the values of the in-plane tensile strengths. Both parameters must be specified and must be positive.
c1 <float>: Specifies the value of the in-plane compressible strength in x-direction. Must be specified and must be positive.
s12 <float>: Specifies the value of the in-plane shear strength. Must be specified and must be positive.
g12|g2p <float>: Specifies the values of the fracture toughness parameters. g12 must be specified while g2p may be omitted. All specified values must be positive.
filter max_of_element: Specifies that for each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index. This option significantly reduces gradient storage requirements and is recommended for use with large meshes with layered materials, where the total amount gradient data can be very large.
fi_min <float>: Specifies the minimum failure index which is required to store the evaluated failure criterion in the database. The default is 0.0, which means that storage is always performed. A value of 0.25 means that storage is performed only when the failure index is greater than or equal to 25%.

In addition to the FAILURE_INDEX Field, the values of the failure criterion evaluated at the element integration points are stored in the FC_LARC04 dataset. For each element integration point, the maximum failure index, the corresponding margin-of-safety, and the number of the failure mode (“component”) are stored: 1 means fiber tensile, 2 fiber compressive, 3 matrix tensile, and 4 means matrix compressive.

Example

material 1 type orthotropic
  # T300/1034-C graphite/epoxy, units in [MPa]
  e1 146.86e+03
  e2 11.376e+03
  e3 11.376e+03
  nu12 0.3
  nu13 0.3
  nu23 0.3
  g1 6.186e+03
  g2 6.186e+03
  g3 6.186e+03

  failure larc04
    t1  1730.0
    t2    66.5
    c1  1379.0
    c2   268.2
    s12  133.763
    g2p    0.23
    g12    0.46
    fi_min 0.5
    filter max_of_element
  end
end

Post-Processing of Failure Criteria

Failure criteria are computed by one of the B2000++ solvers or with Simples and they can be extracted from the model database and visualized with baspl++ or with the B2000++ data browser or with Simples scripts.

baspl++ Examples

The first example script file:fi.py displays the maximum failure index per element:

if len(sys.argv) != 2:
    print 'usage: baspl++ fi.py database'
    sys.exit(1)

m = Model(sys.argv[1])
p = NPart(m)
p.edge.show = True
p.elements.extract = 1
f = Field(m, 'FAILURE_INDEX', case_index=0, cycle_index=-1)
p.contour.colmap.min = 0
p.contour.colmap.max = 1
p.contour.field = f

The next examplescript file:fi.py displays the failure index per element at each element integration point.

if len(sys.argv) != 2:
    print 'usage: baspl++ fi_ip.py database'
    sys.exit(1)

m = Model(sys.argv[1])
p = NPart(m)
p.edge.show = True
p.face.show = False
p.elements.extract = 1
f = Field(m, 'FAILURE_INDEX', case_index=0, cycle_index=-1)
p.sampling.compname = 'fi'
p.sampling.colmap.min = 0
p.sampling.colmap.max = 1
p.sampling.field = f

Heat Flow Materials

The material type heat is used to specify linear and nonlinear material parameters for heat conduction, heat convection, and heat radiation elements. For heat conduction, isotropic and orthotropic materials are supported. Depending whether heat conduction elements or heat convection and heat radiation ‘overlay’ elements reference the material, different parameters may need to be specified.

MDL Specification

material id type heat
  k|k1|k2|k3 ...
  [specific_heat ...]
  [density <float>]
  h_c ...
  diffuse_reflectivity <float>
  emissivity <float>
  stefan_boltzmann_constant <float>
  radiation_reference_temperature <float>
end

Heat Conduction Parameters

k|k1|k2|k3 ...

Specifies the conductivity coefficient in material directions 1, 2 and 3. If k is specified, this means k1=k2=k3=k.

The conductivity can be specified as a constant, as a set of support points for a linear or cubic-spline interpolation, or as a Python expression.

k|k1|k2|k3 <float>
k|k1|k2|k3 interpolated linear|cubic flist
k|k1|k2|k3 function f

For the interpolation, the temperatures and corresponding conductivity coefficients must be specified with a list. Example:

k interpolated cubic [-100.0 8.95 173.15 8.95 273.15 11.5 1623.15 46.
3623.15 51. 5623.15 51. ]

If the conductivity is specified as a Python expression, that expression must be specified as a string, where t is the temperature:

k function '0.3 * t**2'

c_p ...

Defines the specific heat (required for non-stationary analysis). The specific heat can be specified as a constant, as a set of support points for a linear or cubic-spline interpolation, or as a Python expression.

c_p <float>
c_p interpolated linear|cubic flist
c_p function f

density <float>

Specifies the value of the density of the material (required for non-stationary analysis).

Heat Convection Parameters

h_c ...

Specifies the convection coefficient. The convection coefficient can be specified as a constant, as a set of support points for a linear or cubic-spline interpolation, or as a Python expression.

h_c  <float>
h_c interpolated linear|cubic flist
h_c function f

Heat Radiation Parameters

diffuse_reflectivity <float>: Specifies the fraction of incident radiation reflected by the radiating surfaces (in the range of 0.0 to 1.0). The reflection is supposed to be diffuse. Default value is 0.0, i.e. all incoming radiation is absorbed.
emissivity <float>: Specifies the ratio of the energy radiated by the material to the energy radiated by a black body at the same temperature in the range of 0.0 to 1.0. Default value is 0.0, i.e the material does not radiate.
stefan_boltzmann_constant <float>: Specifies the Stefan-Boltzmann constant, must be given according to the units used. Default is 5.6704e-8 for use with S.I. units.
radiation_reference_temperature <float>: Specifies the reference temperature for radiation into the void. Default is 0.0.

Example

material 1 type heat
    k 10.0
    c_p 1000.0
    radiation_reference_temperature 300.
    density 1000.
    emissivity 0.83
    stefan_boltzmann_constant 5.67e-8
end

User Defined Materials

Parameters for user-specific material implementations can be specified in dictionary as follows:

material id type=user material-name
  key k type I|F|S <values>
  key k type I|F|S <values>
end

where material-name is the name of the material implementation under which it is registered. At the beginning of an analysis, the shared library containing the material implementation is located and dynamically loaded, and the material object is instantiated and initialized.

The material parameters are given in key-type-value form, where k must not be longer than 63 characters. type defines the type of <values>: I is a list of`` <int>`` enclosed in [], F a list of <float> enclosed in``[]``, and S a character string.

Gradients

Large FE models, nonlinear analysis, or analysis with layered materials produce very large amounts of gradient data stored in sample point fields. In such situations the amount of data produced can be reduced:

In the material definition, specify a failure criterion and set the option

filter max_of_element

For each element, gradient data (of any kind) is stored only for the integration point with the maximum failure index.
In the material definition, failure criterion and set the option

fi_min <float>

Gradient data is stored only for integration points having a failure index greater than or equal to fi_min.
In the MDL case specification, use the gradients to control at which load increments gradient data is written to the database.

In the following example, the amount of gradient data written to the database is drastically reduced:

material 1 type orthotropic
  # T300/1034-C graphite/epoxy, units in [MPa]
  e1 146.86e+03
  e2 11.376e+03
  e3 11.376e+03
  nu12 0.3
  nu13 0.3
  nu23 0.3
  g1 6.186e+03
  g2 6.186e+03
  g3 6.186e+03

  failure hashin
    t1  1730.0
    t2    66.5
    c1  1379.0
    c2   268.2
    s12  133.763
    s23  101.4
    filter max_of_element # take only the integration point with maximum fi
    fi_min 0.5            # and only if fi >= 0.5
  end
end

case 1
  ebc            1
  analysis       nonlinear
  gradients      -1 # only at the end of the nonlinear analysis
end

Stresses and Strains

Stresses, strains, and any failure criteria computed by B2000++ and stored in the database, are computed at the integration points (“Gauss” points). Stress and strain tensors (see figure below)

\[\begin{split}\begin{align} [\sigma_{ij}] = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ & \sigma_{22} & \sigma_{23} \\ sym & & \sigma_{33} \\ \end{bmatrix} & \; \; \; \;\; \; [\epsilon_{ij}] = \begin{bmatrix} \epsilon_{11} & \epsilon_{12} & \epsilon_{13} \\ & \epsilon_{22} & \epsilon_{23} \\ sym & & \epsilon_{33} \\ \end{bmatrix} \end{align}\end{split}\]

are stored as vectors similar (but not equal!) to the Voight notation:

\[ \begin{align}\begin{aligned}\mbox{B2000++:} \; \;\; \; [\sigma] = \begin{bmatrix} \sigma_{11}, & \sigma_{22}, & \sigma_{33}, & \sigma_{12}, & \sigma_{23}, & \sigma_{13}\ \end{bmatrix}\\\mbox{Voight:} \; \;\; \; [\sigma] = \begin{bmatrix} \sigma_{11}, & \sigma_{22}, & \sigma_{33}, & \sigma_{23}, & \sigma_{13}, & \sigma_{12}\ \end{bmatrix}\end{aligned}\end{align} \]

Tensors (stored as vectors), such as stresses and strains are expressed in the branch global coordinate system. Specifically,

Strains and stresses originating from linear analysis are “engineering” strains and stresses.
Strains originating from nonlinear analysis are Green-Lagrange strains.
Stresses originating from nonlinear analysis are Cauchy stresses.

For the two-dimensional elements, stresses and strains that are stored in the database are expanded to 3D. For plane-stress analysis, the transversal strain \(\epsilon_{33}\) is computed, and for plane-strain analysis, the transversal stress (\(\sigma_{33}\) is computed.

The prismatic and the hexahedral elements support laminate materials (in similar fashion as the shell elements do). In case of laminate materials, the integration scheme is applied to each layer separately. This may result in a large number of integration points per element. For instance, for a hexahedral element HE27.S.TL using the default integration rule GAUSS3X3X3 and a laminate consisting of 10 layers, the number of integration points is 270. When the number of layers is greater than 3 or 4, the integration rule GAUSS3X3X1 (9 integration points per layer instead of 27) can be used instead. See also Integration Schemes.

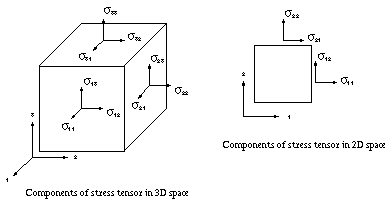
_images/stress-tensor.png — Stress tensor components.

_images/heat-flux.png — Components of heat flux through element faces.