B2000++ Elements

Deformation Analysis Elements

All B2000++ deformation analysis elements are designed for static and dynamic analysis, linear, material-nonlinear, and geometric nonlinear analysis (a Total-Lagrangian approach is employed to account for geometric nonlinearities).

• Rod and Cable Elements

• Beam Elements

• Shell Elements

• 2-dimensional Continuum Elements

• 3-dimensional Continuum Elements (Solid Elements)

• Point Mass Elements

• Rigid-Body (RBE) Elements

• Spring Element

• Distributed Coupling Element

• Shell-to-Solid Coupling Elements

Rod and Cable Elements

The rod/cable elements are designed for static and dynamic, linear and nonlinear analysis of truss and cable structures. The element topology ist described in the Generic Element section.

The Total-Lagrangian approach is employed to allow for arbitrary rigid-body motions.

An initial strain, an initial stress, or an initial force can be applied to rod and cable elements.

Axial stresses, strains, and forces stored on database are all expressed in the element-local coordinate system. For nonlinear analysis, the strain is the Green-Lagrange strain, while the stress is the Cauchy stress. Axial stresses are stored in the STRESS_SECTION_ROD sampling point field datasets. Axial strains are stored in the STRAIN_SECTION_ROD datasets. Axial section forces are stored in the FORCE_SECTION_ROD sampling point field datasets.

Rod and Cable Elements

Name	DOFs [1]	Stresses [2]	Strains [2]	Comment
Rx.S	Ux, Uy, Uz	Sxx	Exx	Displacements in global reference frame

The R2.S is a two-node, fully-integrated rod/cable element. The shape functions are compatible with the B2.S.RS beam element and with the element edges of linear shell and continuum elements.

The R3.S is three-node, fully-integrated quadratic rod/cable element. The shape functions are compatible with the B3.S.RS beam element and with the element edges of quadratic shell and continuum elements.

The R4.S is a four-node, fully-integrated cubic rod/cable element. The shape functions are compatible with the B4.S beam element and with the element edges of cubic shell and continuum elements.

Required MDL Parameters

mid v

Specifies the element material number v (int) for all subsequently specified elements. v remains valid until a new mid parameters is encountered or until the element parameter eltype is specified. Rod (cable) elements can process materials of the following types: isotropic, viscoelastic

area t

Specifies the cross section area t (float). The same definition will be used for all elements defined hereafter until a new area parameter is encountered or until the element parameter eltype is specified.

Optional MDL Parameters

initial_strain_xx v

Defines an initial strain e for subsequently defined beam elements. The initial strain is assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_strain_xx parameter is encountered or until the eltype command is specified.

initial_stress_xx v

Defines an initial stress s for subsequently defined beam elements. The initial stress is assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_stress_xx parameter is encountered or until the eltype command is specified.

initial_force_x v

Defines an initial force f acting at the centroid for subsequently defined beam elements. The initial force is assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_force_x parameter is encountered or until the eltype command is specified.

initial_force_off_x fx my mz

Defines an initial force fx and an initial moment my (around the local y-axis) and an initial moment mz (around the local z-axis) acting at the Centroid of the section. The initial force and the moments are assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_force_off_x parameter is encountered or until the eltype command is specified.

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

non_structural_mass v or nsm v

Defines the non-structural mass per unit length. Default is 0. The same definition will be used for all elements defined hereafter, until a new non_structural_mass parameter is encountered or until a new eltype command is specified.

Beam Elements

The beam elements are designed for static and dynamic, linear and nonlinear analysis. For nonlinear analysis, finite strains are supported. The element topology is described in the Generic Element section. Beam section-specific data are described by the property MDL command. All other beam data are described within the elements block and are describes below.

Beam Elements for Stress Analysis

Name	DOFs [1]	Forces	Moments	Comment
Bx.S	Ux, Ux, Uz, Rx, Ry, Rz	Fx, Fy, Fz	Mx, My, Mz	DOFs in global reference frame, F, M in element-local reference frame.

Beam elements may contain an initial strain, stress, or force and eccentricities. Special means for computing the cross-section constants are available.

Reissner-Simo Beam Elements for Stress Analysis

Element Name	Description
B2.S.RS	A two-node linear prismatic Timoshenko beam element with selective under-integration, according to the Reissner/Simo formulation. The shape functions are compatible with the R2.S rod/cable element and with the element edges of linear shell and continuum elements. This element may not be very accurate for pure bending if only a single element is being used to discretize a thin beam.
B3.S.RS	A three-node quadratic prismatic Timoshenko beam element with selective under-integration, according to the Reissner/Simo formulation. The shape functions are compatible with the R3.S rod/cable element and with the element edges of quadratic shell and continuum elements.

Cubic Beam Elements for Stress Analysis

Element Name	Description
B2.S.E2	A two-node cubic Timoshenko beam element with 2*6 element-internal degrees-of-freedom. The shape functions are not compatible with those of shell or solid elements, except at the beam ends. A straight beam is assumed for the initial configuration. Full integration is conducted with 5-point Gauss-Legendre-Lobatto quadrature. Thus, stresses are calculated also at the beam ends. This element is accurate for pure bending. The behavior of a cubic Euler-Bernoulli beam element can be achieved by setting the shear_correction_factors in the beam property to a high value.
B4.S	A four-node cubic Timoshenko beam element. The shape functions are compatible with the R4.S rod/cable element and with the element edges of cubic shell and continuum elements. Full integration is conducted with 5-point Gauss-Legendre-Lobatto quadrature. Thus, stresses are calculated also at the beam ends. This element is accurate for pure-bending if it is not curved in the initial configuration and if the nodes are equidistant. The behavior of a cubic Euler-Bernoulli beam element can be achieved by setting the shear_correction_factors in the beam property to a high value.

Forces and moments stored in the database are all expressed in the element-local coordinate system. For linear analysis, the strains and stresses are the “engineering” stresses and strains. For nonlinear analysis, the strain is the Green-Lagrange strain, while the stress is the Cauchy stress.

Forces and moments are evaluated and stores at the Gauss integration points. They can be extrapolated to the nodes defining the beam in a post-processing step.

Note

Stresses and strains of beam elements are not computed by the B2000++ solvers and must be evaluated a posteriori with a tool such as Simples or baspl++.

non_structural_mass or nsm of Bx.S.RS elements must be specified in the beam property block.

Required MDL Parameters

beam_orientation x y z

Defines the beam orientation vector in the beam-local x-y plane. The same definition will be used for all elements defined hereafter, until a new beam_orientation parameter is encountered or until the eltype command is re-specified.

beam_orientation refnode v

Defines the (external) beam reference node v (positive int). The reference node defines a vector in the beam local x-y plane together with the first beam node. The same definition will be used for all elements defined hereafter, until a new beam_orientation parameter is encountered or until the eltype command is specified. See also Generic Beam Elements for the definition of the beam reference node.

pid v

Specifies the beam property identifier (positive int) pointing to the beam property table. The same definition will be used for all elements defined hereafter, until a new value v is encountered or until a new element type is specified.

Optional MDL Parameters

beam_offsets x1 y1 z1  x2 y2 z2 ...

Defines the beam eccentricities (or offsets) for all nodes defining the beam, for subsequently defined beam element. x, y, and z are defined with respect to the branch reference frame. The same definition will be used for all elements defined hereafter, until a new beam_offsets parameter is encountered or until the eltype command is specified. See also Generic Beam Elements for the definition of the beam eccentricities.

beam_dof_release1 pattern | clear

Release part of the element’s connections to the degrees-of-freedom at the first node. The degrees-of-freedom to be released are specified w.r.t. the beam-local coordinate system. pattern is a concatenated string containing the degrees of freedom (1, 2, 3, 4, 5, or 6) to be released. clear removes all releases (i.e., nothing is released). The same definition will be used for all elements defined hereafter, until a new beam_dof_release1 parameter is encountered or until the eltype command is specified. Example:

beam_dof_release1 456

releases all rotational degrees of freedom.

beam_dof_release2 pattern | clear

Release part of the element’s connections to the degrees-of-freedom at the second node. The degrees-of-freedom to be released are specified w.r.t. the beam-local coordinate system. pattern is a concatenated string containing the degrees of freedom (1, 2, 3, 4, 5, or 6) to be released. clear removes all releases (i.e., nothing is released). The same definition will be used for all elements defined hereafter, until a new beam_dof_release2 parameter is encountered or until the eltype command is specified. Example:

beam_dof_release2 4

releases the rotational degree-of-freedom of the beam end node around the beam-local x-direction (the beam axis).

initial_strain_xx v

Defines an initial strain e for subsequently defined beam elements. The initial strain is assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_strain_xx parameter is encountered or until the eltype command is specified.

initial_stress_xx v

Defines an initial stress s for subsequently defined beam elements. The initial stress is assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_stress_xx parameter is encountered or until the eltype command is specified.

initial_force_x v

Defines an initial force f acting at the centroid for subsequently defined beam elements. The initial force is assumed constant along the element x-axis. The same definition will be used for all elements defined hereafter, until a new initial_force_x parameter is encountered or until the eltype command is specified.

Shell Elements

The shell elements are designed for static and dynamic, linear and nonlinear analysis of thin- and thick-walled plate and shell structures with isotropic, orthotropic and laminated, linear and nonlinear materials. The element topology is described in the Generic Element Section for triangular and quadrilateral elements.

Shell Elements for Stress Analysis

Name	DOFs [1]	Stresses [2]	Strains [2]	Comment
Tx.S.MITC	Ux, Uy, Uz, Rx, Ry, Rz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz
Qx.S.MITC	Ux, Uy, Uz, Rx, Ry, Rz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz
Q4.S.MITC.E4	Ux, Uy, Uz, Rx, Ry, Rz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Like the Q4.S.MITC element, but with 4 incompatible modes for in-plane bending.

The shell elements are based on Reissner-Mindlin shell theory and have 5 or 6 degrees of freedom per node. To account for geometric nonlinearity, a Total-Lagrangian approach is employed. The MITC (Mixed Interpolation of Tensorial Components) formulation (see [Bathe96], [BatheMITC]) improves the out-of-plane behavior by interpolating the through-the-thickness term of the strain tensor differently. This is a better way for preventing out-of-plane locking than selective under-integration. The rotation of the director is computed by making use of finite rotations to allow for computing the director of the deformed configuration directly by an algebraic expression of the rotational degree of freedoms, i.e without numeric integration.

For laminates involving linear materials for all layers, the shell elements automatically perform the through-the-thickness integration a priori in analytical fashion. Hence, the number of layers is irrelevant to the computation time of the first and second variations. The benefit of this optimization is a considerable speed-up for analysis of composite structures. Note that this optimization does not alter the element response.

Stresses, strains, and any failure criteria which are stored in the database, are computed at the integration points (“Gauss” points) which are used by the element to compute the first and second variations. The stresses and strains which are stored in the database are all expressed in the branch global coordinate system. For linear analysis, the strains and stresses stored in the database are the “engineering” stresses and strains. For nonlinear analysis, the strain is the Green-Lagrange strain, while the stress is the Cauchy stress. The in-plane integration rule depends on the element type. For the through-the-thickness integration, a 3-point Gauss-Legendre-Lobatto rule is used (for laminates, this applies to each layer). This rule ensures that gradients are evaluated at the surfaces and at the layer boundaries, thus, where the maximum strains and stresses occur.

The Q9.S.MITC element is more effective (i.e. it has a better ratio of accuracy vs. computational effort) than the other B2000++ shell elements, even for highly-distorted meshes. This element should be considered whenever a new FE model is being made. The Q8.S.MITC element is intended for FE models that were imported from other FE codes that do not support nine-node quadrilateral elements.

Due to the incompatible modes, the Q4.S.MITC.E4 element does not pass the patch tests (i.e. cannot exactly represent constant strain fields), and it may exhibit instabilities in buckling analysis and in nonlinear analysis. Elements of this type should not be significantly distorted. While the in-plane bending response of this element is better than the Q4.S.MITC element, the latter gives more predictable results, especially concerning the gradients.

For the the quadratic MITC elements (T6.S.MITC, Q8.S.MITC, Q9.S.MITC), mid-edge and mid-face nodes should be located at the middle of the edges and centre of the face, respectively. Otherwise, the Jacobian will contain higher-order terms, and the elements will not work with full accuracy. However, for moderately curved geometries such as cylindrical panels, the error is small enough that the accuracy is still very good.

The T6.S.MITC element fails for certain double-curved geometries such as hyperboloid shells. Further, for complex loading conditions, this element may exhibit instabilities which affect the accuracy of the linearized buckling load (i.e. the predicted buckling load will be too low for coarse meshes).

Required MDL Parameters

mid v

Specifies the element material number v (int) for all subsequently specified elements. v remains valid until a new mid parameters is encountered or until the element parameter eltype is specified. Rod (cable) elements can process materials of the following types: isotropic, laminate, orthotropic, isotropic viscoelastic, orthotropic viscoelastic

nthickness t1 t2  t3 ...

Specifies the element’s thickness at each of the element’s nodes. This parameter allows to specify varying element thickness. The element thickness is interpolated using the element’s in-plane shape functions. Not required for laminate materials.

thickness t

Specifies a constant element thickness t. Not required for laminate materials.

Optional MDL Parameters

eccent e

Defines the element eccentricity e, which is a constant offset of the shell volume w.r.t. the shell reference surface. The same units as for the coordinates and thicknesses are used. Default is 0. With \(e = \frac{1}{2}t\), where t is the shell thickness, the shell bottom surface coincides with the shell reference surface. With \(e = - \frac{1}{2}t\), the shell top surface coincides with the shell reference surface.

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

morientation default

Resets to the default material orientation which is obtained by projecting the branch-global x-direction onto the shell surface and constructing an orthogonal reference frame (this will not work for elements whose shell surface normal is aligned with the x-direction).

morientation ... end

Specifies the material orientation, see morientation.

neccent e1 e2 e3 ...

Defines the nodal eccentricities e (float), which are the offset of the shell surface from the shell reference surface, at the nodal position(s). This command allows to specify varying eccentricity. The element eccentricity is interpolated using the element’s in-plane shape functions. Otherwise, the definition is similar to eccent.

non_structural_mass v

Defines the non-structural mass per unit area. Default is 0. The same definition will be used for all elements defined hereafter, until a new non_structural_mass parameter is encountered or until the eltype command is specified.

Optional MDL Parameters

drills f

Defines the “drill” stiffness factor v (float) for shell element nodes with 6 degrees-of-freedom and whose in-plane rotation (drill) will be stabilized. Default is 1e-8. The effective drill stiffness is calculated using the averaged in-plane shear modulus and the element configuration and thickness, and is multiplied with f. Hence, a value of 0 for f means no drill stabilization. The section Shell Elements and the Drill Stiffness contains additional information on the problem of the drill stiffness.

drills applies only to the 6th degree of freedom of shell elements that may need stabilization, in contrast to the autospc parameter in conjunction with the (see MUMPS sparse linear solver)

Two-Dimensional Continuum Elements

The two-dimensional elements support plane-stress and plane-strain assumptions (whether the element will be used for plane-stress or plane-strain analysis, must be indicated in the material definition). Some elements support laminates. The mixed elements are implemented according to [Sussman87] and [Bathe96] and can be applied to quasi-incompressible materials.

Two-dimensional Elements for Stress Analysis

Name	DOFs [1]	Stresses [2]	Strains [2]	Comment
Tx.S.2D.TL	Ux, Uy	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Pure displacement formulation elements.
T6.S.2D.UP3	Ux, Uy	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation elements with linear internal pressure field. They pass the inf-sup test.
Qx.S.2D.TL	Ux, Uy	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Pure displacement formulation elements.
Q4.S.2D.E4	Ux, Uy	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Enhanced-assumed strain (EAS) formulation with four incompatible modes.
Qx.S.2D.UP1	Ux, Uy	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation with constant internal pressure field. They do not pass the inf-sup test.
Q9.S.2D.UP3	Ux, Uy	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation elements with linear internal pressure field. They pass the inf-sup test.

When using mixed elements with quasi-incompressible materials, the global stiffness matrix becomes nearly non-definite. The default sparse linear solver, dmumps, can handle such matrices, but other sparse linear solvers may not work (see Sparse Linear Solvers :ref:`solvers.sls).

Stresses, strains, and any failure criteria which are stored in the database, are computed at the integration points (“Gauss” points) which are used by the element to compute the first and second variations. The stress and strain tensors stored in the database are all expressed in the branch-global coordinate system. For linear analysis, the strains and stresses stored in the database are the “engineering” stresses and strains. For nonlinear analysis, the strain is the Green-Lagrange strain, while the stress is the Cauchy stress. The in-plane integration rule depends on the element type. For the through-the-thickness integration, a 3-point Gauss-Legendre-Lobatto rule is used (for laminates, this applies to each layer). This rule ensures that gradients are evaluated at the surfaces and at the layer boundaries, thus, where the maximum strains and stresses occur.

Required MDL Parameters

mid v

Specifies the element material number v (int) for all subsequently specified elements. v remains valid until a new mid parameters is encountered or until the element parameter eltype is specified. Rod (cable) elements can process materials of the following types: isotropic, laminate, orthotropic, isotropic viscoelastic, orthotropic viscoelastic

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

morientation default

Resets to the default material orientation which is obtained by projecting the branch-global x-direction onto the shell surface and constructing an orthogonal reference frame (this will not work for elements whose shell surface normal is aligned with the x-direction).

morientation ... end

Specifies the material orientation, see morientation.

Solid Elements

The solid elements elements are designed for static and dynamic, linear and nonlinear analysis of solids. The elements are formulated with the Total Lagrangian formulation, see [Bathe96]. The element topology ist described in the Generic Element Section for tetrahedral, hexahedral, and prismatic elements.

Solid Elements for Stress Analysis

Name	DOFs [1]	Stresses [2]	Strains [2]	Comment
TEx.S.TL	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Pure-displacement formulation. x=4,10
TE10.S.UP4	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation with linear internal pressure field. Passes the inf-sup test.
PRx.S.TL	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Pure-displacement formulation. Supports laminates. x=6,15
HExS.TL	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Pure-displacement formulation. Supports laminates. x=8,20,27
HE8.S.E9	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Enhanced-assumed strain (EAS) formulation with nine incompatible modes. Supports laminates.
HE8.S.UP1	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation with constant internal pressure field. Does not pass the inf-sup test.
HE20.S.UP1	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation with constant internal pressure field. Passes the inf-sup test.
HE27.S.UP4	Ux, Uy, Uz	Sxx, Syy, Szz, Sxy, Syz, Sxz	Exx, Eyy, Ezz, Exy, Eyz, Exz	Mixed formulation with linear internal pressure field. Passes the inf-sup test.

All solid elements support isotropic, orthotropic and also layered materials. For laminates involving linear materials for all layers, the shell elements automatically perform the through-the-thickness integration once in an analysis.

All elements are isoparametric. The nodal degrees-of-freedom are the displacements. All elements pass the MacNeal-Harder patch test (i.e. they can represent a constant strain field exactly).

HE8.S.E9 elements may exhibit instabilities in nonlinear analysis, due to the incompatible modes. Elements of these types should not be significantly distorted.

When using mixed elements with quasi-incompressible materials, the global stiffness matrix becomes nearly non-definite. The default sparse linear solver, dmumps, can handle such matrices, but other sparse linear solvers may not work (see Sparse Linear Solvers :ref:`solvers.sls).

Stresses, strains, and any failure criteria which are stored in the database, are computed at the integration points (“Gauss” points) which are used by the element to compute the first and second variations. The stresses and strains which are stored in the database are all expressed in the branch global coordinate system. For linear analysis, the strains and stresses stored in the database are the “engineering” stresses and strains. For nonlinear analysis, the strain is the Green-Lagrange strain, while the stress is the Cauchy stress. The in-plane integration rule depends on the element type. For the through-the-thickness integration, a 3-point Gauss-Legendre-Lobatto rule is used (for laminates, this applies to each layer). This rule ensures that gradients are evaluated at the surfaces and at the layer boundaries, thus, where the maximum strains and stresses occur.

Required MDL Parameters

mid v

Specifies the element material number v (int) for all subsequently specified elements. v remains valid until a new mid parameters is encountered or until the element parameter eltype is specified. Rod (cable) elements can process materials of the following types: isotropic, laminate, orthotropic, isotropic viscoelastic, orthotropic viscoelastic

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

morientation default

Resets to the default material orientation which is obtained by projecting the branch-global x-direction onto the shell surface and constructing an orthogonal reference frame (this will not work for elements whose shell surface normal is aligned with the x-direction).

morientation ... end

Specifies the material orientation, see morientation.

Point Mass Elements

A point mass element defines masses and mass moments of inertia at a mesh node, with respect to the node-local coordinate system, see transformations and nodes commands.

• For static analysis the point masses will be used to compute inertia forces.

• For dynamic analysis point mass will be added to the global mass matrix.

The point mass elements PMASS3.S and PMASS6.S work for linear and geometric nonlinear analysis.analysis.

Point Mass Elements for Stress Analysis

Name	Comment
PMASS3.S	Adds mass forces to 3 translational DOFs.
PMASS6.S	Adds mass forces to 3 translational DOFs and mass moments to the 3 rotation DOFs of a node.

Required MDL Parameters

mass m

Specifies the ‘lumped’ nodal mass m (float) of PMASS3.S and PMASS6.S elements. mass remains defined until a new mass parameter is specified or until a new eltype parameter is specified.

matrix m11 m12 m22 m13 m23 m33 m14 m24 m34 m44 m15 m25 m35 m45 m55 m16 m26 m36 m46 m56 m66

Specifies the coefficients of the symmetric nodal mass coefficient matrix, i.e the 21 terms stored column-wise (upper triangle of matrix) of PMASS6.S elements. If matrix is specified, mass, inertia_moments, and offsets may not be specified, and vice versa.

inertia_moments Ixx Iyy Izz Ixy Iyz Ixz

Specifies the components of the inertia moment tensor, expressed in the branch-global coordinate system (PMASS6.S ements). The inertia moments are 0 by default.

offsets ox oy oz

Specifies the offset, in each direction, of the mass point with respect to the node (PMASS6.S elements). The default offset \(o\) in each direction is 0.

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

Mass Matrix

The mass matrix is computed as follows for a PMASS6.S element:

\begin{equation} \begin{bmatrix} m & 0 & 0 & 0 & mo_z & -mo_y \\ & m & 0 & -mo_z & 0 & mo_x \\ & & m & mo_y & -mo_x & 0 \\ & & & I_{xx}+mo_z^2+mo_y^2 & -I_{xy}-mo_xo_y & -I_{xz}-mo_yo_z \\ & & & & I_{yy}+mo_z^2+mo_y^2 & -I_{yz}-mo_yo_z \\ & & & & & I_{zz}+mo_y^2+mo_x^2 \end{bmatrix} \end{equation}

Example

Define masses of 10000 in each of the three translation directions for node 45 and 230 and masses of 50000 each of the three translation directions for node 457 (note the PMASS3.S element identifiers are 1, 2, and 3, respectively):

elements
   eltype pmass3.s
   mass 10000
   1 45
   2 230
   mass 50000
   3 457
end

Rigid-Body (RBE) Elements

The “rigid-body” element couples the displacement and the rotational degrees-of-freedom of one or several slave nodes with the displacement and rotational degrees-of-freedom of the master node in such a way that this corresponds to a rigid-body motion.

Because the number of connected nodes is not fixed, the element connectivity has to be enclosed by square brackets “[” and “]”. The master node is specified first, followed by the slave nodes. For mesh-independent definitions, the slave nodes can be specified by means of nodesets.

MDL Specification

elements
    ...
    type RBE
    element-id [ n0 (dof pattern) n1 n2 ... ]
    element-id [ n0 (dof pattern) nodeset nid ]
    element-id [ n0 (dof pattern) epatch epatch-id e1-e12|f1-f7|b ]
    ...
end

The degrees-of-freedom of the slave nodes to be coupled can be specified optionally, by means of the dof parameter. pattern (int) contains the digits 1-6, corresponding to the Ux, Uy, Uz, Rx, Ry, Rz degrees-of-freedom. For example, 123 means all displacement degrees-of-freedom, and 123456 means all displacement and rotation degrees-of-freedom. The default 123456 will be applied, unless dof is specified. Once set, the specified DOF will be applied to any subsequent slave nodes until a new dof parameter is given.

Example

This example demonstrates the use of dof and of node sets. A cylindrical shell made of aluminum with a radius of 2 m , a length of 10 m and a thickness of 2.5 mm is clamped at one end and shall be subjected to a bending force applied at the other end. The axis of the cylinder coincides with the z-direction. Both ends are connected to an RBE element. One end is fixed (condition ebc 1), while an axial force is applied to the other end (condition nbc 1).

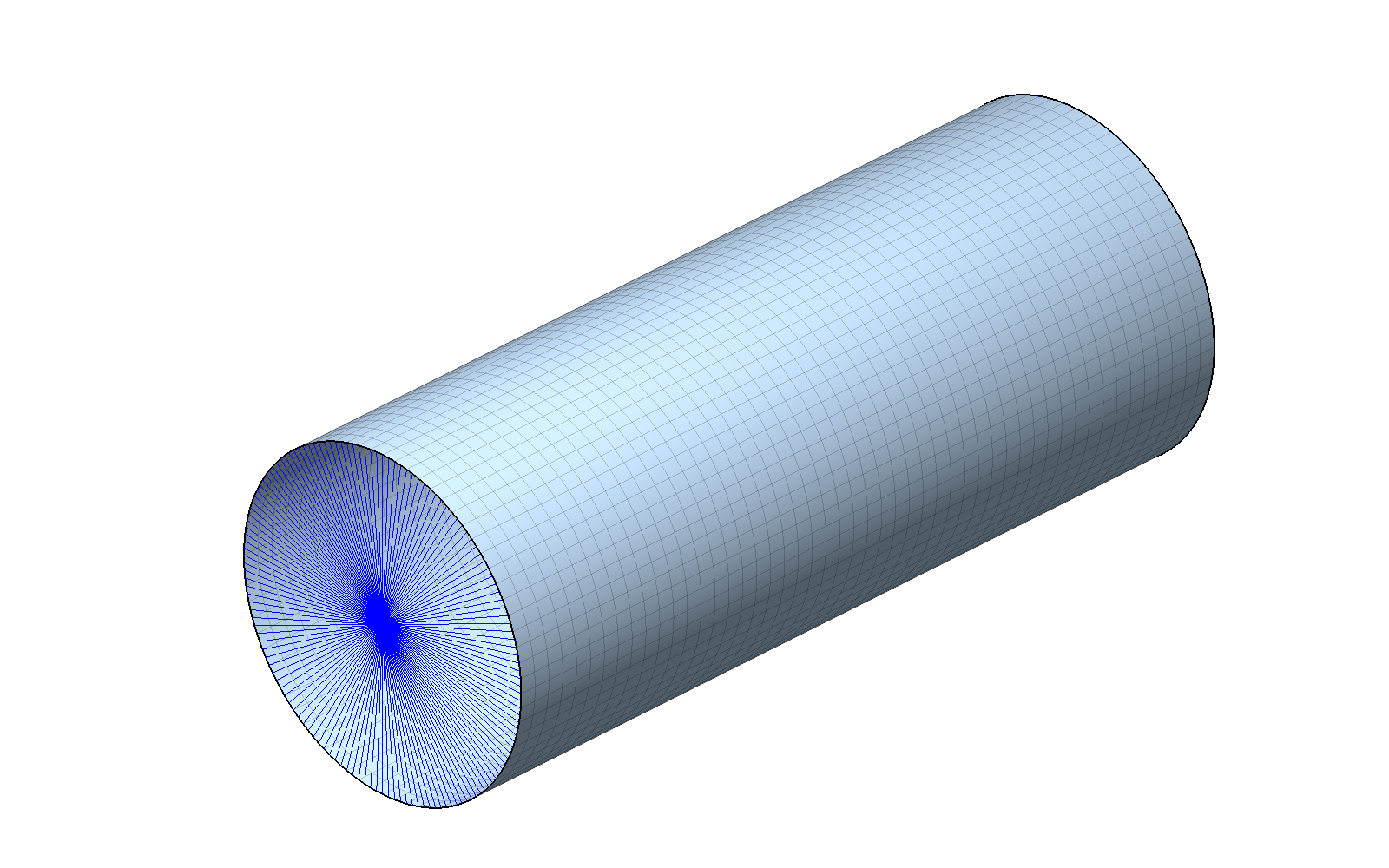
Cylinder mesh and one of the two RBE elements.

The MDL problem definition file is listed below:

epatch 1
  geometry cylinder
  radius 2.0 thickness 0.0025 phi1 0.0 phi2 360.0 length 10.0
  local all
  ne1 72
  ne2 50
  eltype Q9.S.MITC
  mid 1
end

material 1 type isotropic
  # Aluminium 2024-T3
  e 72.4e9
  nu 0.33
  density 2800.
  alpha 22.8e-6 # [1/K]
  failure von_mises
    r 138e6
    filter max_of_element
  end
end

nodes
  100000 0. 0.  0.
  100001 0. 0. 10.
end

elements
  type RBE
  100000 [100000  dof 23456  epatch 1 e1]
  100001 [100001  dof 23456  epatch 1 e3]
end

ebc 1
  dof [Ux Uy Uz Rx Ry Rz] value 0. node 100000
end

nbc 1
  dof FZ value -1e6 node 100001
end

case 1
  analysis  linear
  ebc       1
  nbc       1
  gradients 1
end

adir
  cases 1
end

Note that the epatch command is used to generate a cylindrical mesh, here with Q9.S.MITC shell elements. The parameter local all generates local reference frames (cylindrical coordinates) for all nodes, with the first direction aligned with the radial direction.

With the above definition the nodes move freely in the radial direction. Alternatively, the RBE elements can be specified such that the radial displacements of the slaves are fixed:

elements
  type RBE
  100000 [100000  dof 123456  epatch 1 e1]
  100001 [100001  dof 123456  epatch 1 e3]
end

The displacement field is compared for the two models in the following figure.

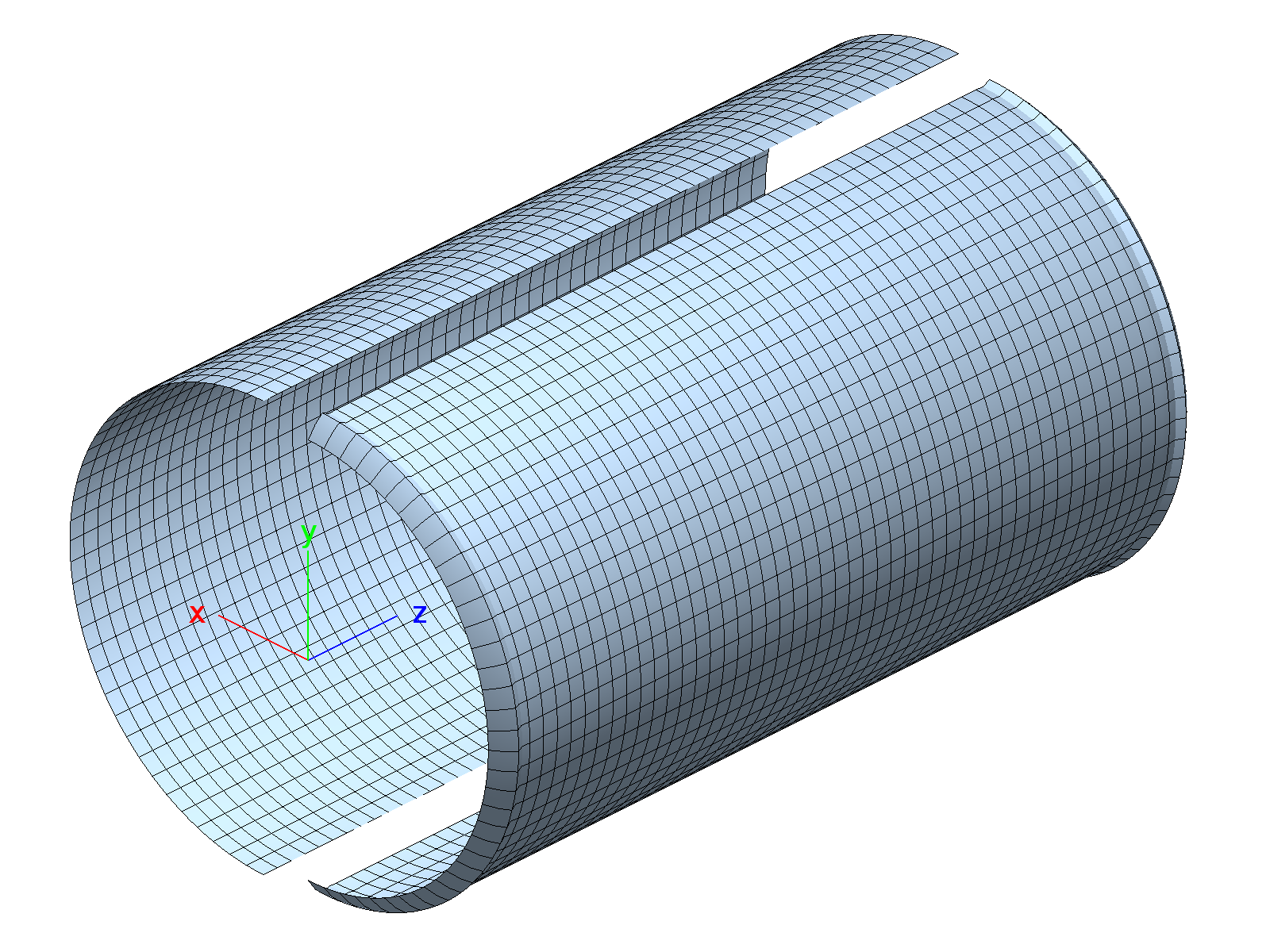
Axially-compressed cylinder (linear analysis, deformations are amplified). Left: The radial displacement DOFs are not coupled. Right: All slave DOFs are coupled.

Spring Element

The scalar spring element connects two nodal degrees-of-freedom and, in dynamic analysis, their velocities:

\[F = K\left( u_{1} - u_{2} \right) + D\left( v_{1} - v_{2} \right)\]

The element is linear and works with the branch-global coordinate system, i.e., it ignores any node-local coordinate systems. If only one degree-of-freedom is specified, this will be connected to the ground:

\[F = Ku_{1} + Dv_{1}\]

If a translation degree-of-freedom (Ux, Uy, or Uz) is specified, that node will have 3 degrees-of-freedom. If a rotation degree-of-freedom (Rx, Ry, or Rz) is specified, that node will have 6 degrees-of-freedom. In this case it may be necessary to lock the degrees-of-freedom that are not connected.

If a node-local coordinate system is defined on the node, and system local is specified, the spring translation or rotation is in that node-local coordinate system.

MDL Specification

 elements
     type SPRING
     element-id [ K kcoeff (D dcoeff) node n1 dof dof1 (system branch|local)]
     element-id [ K kcoeff (D dcoeff) node n1 dof dof1 (system branch|local) node n2 dof dof2 (system branch|local)]
 end

The element stiffness K (float) must be specified. The damping
coefficient D is optional and has a default value of 0.

Example

Two spring elements connect degrees-of-freedom Ux (translation in X-direction) and Ry (rotation around the Y-axis) of node 1 to the ground. No damping coefficients are specified, thus, the default value of zero will be used. There is also a point-mass element defined at that node. The node could be connected by an RBE element to other parts of a FE model. This is not the case here, therefore, the degrees-of-freedom not connected are locked.

nodes
  1  0. 0. 0.
end

elements
  type SPRING
  1 [k 20000.    node 1 dof Uz]
  2 [k 17391.125 node 1 dof Ry]

  type PMASS6.S
  matrix [
  0.   0.   0.   0.   0.     0.
       0.   0.   0.   0.     0.
            2.   0.   -1.8   0.
                 0.   0.     0.
                      1.7391 0.
                             0.
  ]
  3  1
end

ebc 1
  dof [Ux Uy Rx Rz] value 0. node 1
end

FMDE Elements

The distributed coupling element connects the degrees-of-freedom at a slave node with those at one or several master nodes, according to the master node weights. Which degrees-of-freedom (DOF) are coupled, depends on the DOF specification.

Because the number of connected nodes is not fixed, the element connectivity has to be enclosed by square brackets […]. The slave node identifier ns` (int) is specified first, followed by one or more master node identifiers nm (int). For mesh-independent definitions, the master nodes can be specified by means of nodesets.

MDL Specification

elements
  type FMDE
  element-id [ (dof v) ns master-node-list ]
  ...
end

The master nodes list can consist of individual node identifiers, optionally preceded by a weight:

(weight w1) mn1 (weight w2) mn2 ...

Master nodes can be specified with one or more nodesets:

(weight w) nodeset id

where id is the nodeset name (string). Master nodes can be also specified with one or more epatch edge, face or body node lists:

(weight w) epatch id e1-e12|f1-f7|b

where id is the epatch identifier (int) and e an edge number, f a face number or b the body.

The degrees-of-freedom to be coupled can be specified optionally, by means of the dof parameter. It takes an integer number v which contains the digits 1-6, corresponding to the Ux, Uy, Uz, Rx, Ry, Rz degrees-of-freedom. For example, 123 means all displacement degrees-of-freedom, and 123456 (default) means all displacement and rotation degrees-of-freedom.

If a weight w (float) is specified (default is 1.0), it will be applied to any subsequent master nodes until a new weight is specified.

SSC Shell-to-Solid Coupling Elements

Shell-to-solid coupling (SSC) elements couple discontinuous shell and solid meshes. In this case the interpolated displacements between shell and solid elements cannot be made wholly continuous. For this reason, the goal is to minimize the difference rather than to eliminate it.

This scenario is typically found in global-local analyses where the global part of the model consists of shell elements while the local part consists of solid elements. Usually, the local part is meshed much finer.

This section describes the SSC elements and how they can be generated automatically.

Alternatively, the field_transfer method can be employed for shell-to-solid coupling. While the SSC elements constitute a point-wise coupling, field_transfer performs a weighted-residual coupling.

Requirements and implementation

In addition to different element sizes and node positions, the shell-to-solid coupling must also account for the transformation of the rotational degrees-of-freedom of the shell elements to the translation degrees-of-freedom of the connected solid elements. This coupling depends on how the shell element directors are calculated from the degrees-of-freedom, a procedure which is specific to the shell element’s formulation and implementation. Hence, the shell-to-solid coupling must be tailor-made for each type of shell element.

In geometrically nonlinear analysis, large rigid-body motions may occur. The shell-to-solid coupling must be performed such that the coupling between the degrees-of-freedom is performed taking into account the current (rotated) configuration. Hence, a linear approach such as enforcing minimal displacement discontinuity by means of the linc will fail.

For these reasons, shell-to-solid coupling in B2000++ is implemented in the form of Finite Elements which (a) are specifically made for each supported shell element type, and (b) support geometrically nonlinear analysis. This allows for incorporating the coupling in the standard solution procedures involving the computation of the first and second variation.

The shell-to-solid coupling elements for the MITC shell elements in B2000++ enforce their constraints using B2000++’s constraint system. By default, the Augmented Lagrange method is used for the static linear and nonlinear solvers, and the Lagrange method is used for the dynamic nonlinear solver. See Linear and Nonlinear Constraint Control for details.

Automatic definition of SSC elements

When the add_ssc_elements parameter is specified in the adir command the B2000++ input processor b2ip++` will automatically add the necessary SSC elements. In that case the explicit definition of SSC elements in the MDL file is not necessary. Example:

adir
  case 1
  add_ssc_elements
end

The criteria defining when and how these elements are added are based on the evaluation of geometrical properties; in particular, the volume element’s node must lie (within sufficient tolerance) in the plane defined by the shell element’s edge. Thus, this automatic procedure is limited to straight and moderately curved shell elements.

Instead of having the SSC elements added automatically, the SSC elements also can be specified explicitly in the MDL file. This is described in the following.

SSC element connectivity

The shell-to-solid coupling elements are rigid and have no materials associated to them. They connect a single edge of a shell element with a single node of 3D solid element. Hence, all nodes of all adjacent solid element’s faces must have a separate coupling element associated.

Edge to solid coupling.

In the above figure, a shell element defined by nodes \(n_1, n_2, n_3, n_4\) is to be linked to a solid element face defined by nodes \(a, b, c, d\). The link is defined such that the solid element face (green) deforms in the same plane as the shell edge (defined by nodes \(n_1, n_2\) in the above figure), the shell edge deforming according to the shell node directors (dashed blue lines). Thus, for the above configuration, 4 coupling elements must be defined, each of them connecting the shell nodes \(n_1, n_2, n_3, n_4\) to one of the solid face nodes 1-4:

\begin{equation} \begin{bmatrix} n_1 & n_2 & n_3 & n_4 & a n_1 & n_2 & n_3 & n_4 & b n_1 & n_2 & n_3 & n_4 & c n_1 & n_2 & n_3 & n_4 & d \end{bmatrix} \end{equation}

The element node connectivity sequences of all coupling elements are specified with first specifying the N nodes defining the shell followed by one of the solid element nodes k:

n1  n2 ... nN  k

n1 to nN are the nodes defining the shell element according to the element connectivity definition of the specific shell element, with the following modification: n1 and n2 are nodes defining the shell element edge to be coupled to the solid. This means that in some cases the original shell element connectivity and the connectivity can be permuted! k is the k-th element node connectivity index of the solid element involved in the coupling process.

Shell-to-solid coupling element

Element Name	Description
SSC.T3.S.MITC	Shell-to-solid coupling element linking a T3.S.MITC triangular shell element to a single node of a 3D solid element. The solid element node will deform with the edge of the shell element defined by the first 2 nodes in the element connectivity list.
SSC.T6.S.MITC	Shell-to-solid coupling element linking a T6.S.MITC second-order triangular shell element to a single node of a 3D solid element. The solid element node will deform with the edge of the shell element defined by the first 2 nodes in the element connectivity list.
SSC.Q4.S.MITC	Shell-to-solid coupling element linking a Q4.S.MITC quadrilateral shell element to a single node of a 3D solid element. The solid element node will deform with the edge of the shell element defined by the first 2 nodes in the element connectivity list.
SSC.Q8.S.MITC	Shell-to-solid coupling element linking a Q8.S.MITC second-order quadrilateral shell element to a single node of a 3D solid element. The solid element node will deform with the edge of the shell element defined by the first 2 nodes in the element connectivity list.
SSC.Q9.S.MITC	Shell-to-solid coupling element linking a Q9.S.MITC second-order quadrilateral shell element to a single node of a 3D solid element. The solid element node will deform with the edge of the shell element defined by the first 2 nodes in the element connectivity list.

Example of SSC definition in the MDL file

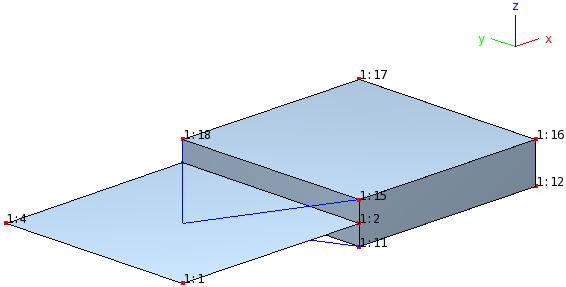
The following simple example demonstrates how SSC elements can be used. It consists of a single quadrilateral shell element which is to be connected to a single hexahedral solid element. The thickness of the shell element is equal to that of the solid element, and the positions in the x- and y-direction at the interface coincide. Note that this is not required, there may be multiple solid elements in the thickness and also multiple solid elements in the y-direction.

The SSC elements are displayed as blue lines going from the node of the 3D solid element to the center of the shell element.

title "2-element SSC example"

nodes
   1  -1.0  0.0  0.0
   2   0.0  0.0  0.0
   3   0.0  1.0  0.0
   4  -1.0  1.0  0.0
  11   0.0  0.0 -0.1
  12   1.0  0.0 -0.1
  13   1.0  1.0 -0.1
  14   0.0  1.0 -0.1
  15   0.0  0.0  0.1
  16   1.0  0.0  0.1
  17   1.0  1.0  0.1
  18   0.0  1.0  0.1
end

elements
  type Q4.S.MITC mid 1 thickness 0.2
  1  1 2 3 4
  type HE8.S.TL mid 1
  2  11 12 13 14 15 16 17 18
  type SSC.Q4.S.MITC
  3  2 3 4 1 11
  4  2 3 4 1 14
  5  2 3 4 1 15
  6  2 3 4 1 18
end

material 1 type isotropic
  e 73.1e3
  nu 0.3
end

ebc 1
  dof [Ux Uy Uz Rx Ry Rz]  value 0.0  nodes [1 4]
end

nbc 1
  dof FZ  value 1.0  nodes [12 13 16 17]
end

case 1
  analysis  linear
  ebc       1
  nbc       1
end

adir
  case 1
end

Heat-transfer Analysis Elements

Th heat transfer analysis elements allow for solving linear, nonlinear, stationary and non-stationary heat transfer problems.

Note

Heat transfer elements and deformation analysis elements cannot be mixed in a single case. Coupled heat analysis and deformation analysis problems must be solver separately, with a staggered scheme.

The B2000++ Examples and Verification document describes heat analysis and coupled heat and deformation analysis problems.

2D Heat Conduction Elements

All heat conduction elements are isoparametric. The degrees-of-freedom are the temperatures at the element nodes. The gradients are the heat fluxes in the global x- and y-direction.

Heat Conduction Elements in \(\mathbf{R}^2\)

Name	DOFs [1]	Heat flux [2]	Comment
Tx.HEAT.CONDUCTION	T	Hx, Hy, Hz	Triangular heat analysis elements, x=3,6.
Qx.HEAT.CONDUCTION	T	Hx, Hy, Hz	Quadrilateral heat analysis elements, x=4,8,9.

Required MDL Parameters

mid v

Specifies the element material number v (int). The referenced material must be of type `heat.

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

3D Heat Conduction Elements

All heat conduction elements are isoparametric. The degrees-of-freedom are the temperatures at the element nodes. The gradients are the heat fluxes in the global x-, y-, and z-direction.

Required MDL Parameters

mid v

Specifies the element material number v (int). The referenced material must be of type `heat.

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

1D Convection and Radiation Overlay Elements

The one-dimensional wire elements and the two-dimensional surface elements for specifying convection and radiation conditions (von Neumann conditions) are ‘overlay’ elements, i.e. they are added to edges or faces of heat conduction element and they do not have own degrees of freedom. All convection and radiation elements are isoparametric.

One-dimensional Heat Convection and Heat Radiation Overlay Elements

Element Name	Description
Lx.HEAT.RADCONV	Line elements, x=2,3

Required MDL Parameters

mid v

Specifies the element material number v (int). The referenced material must be of type `heat.

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

Convection and Radiation Overlay Elements

Heat Convection and Heat Radiation Overlay Elements

Element Name	Description
Lx.HEAT.RADCONV	Line elements, x=2,3
Tx.HEAT.RADCONV	Triangular elements, x=3,6,7
Qx.HEAT.RADCONV	Quadrilateral elements, x=4,8,9

Required MDL Parameters

mid v

Specifies the element material number v (int). The referenced material must be of type `heat.

Optional MDL Parameters

group gid

Defines the element group number gid (non-negative int). The default group number is 0. The same definition will be used for all elements defined hereafter, until a new group parameter is encountered or until the eltype command is specified.

Element Material Orientation

The element material orientation specification of MDL defines the orientation of materials with respect to references systems. There are two methods for defining the material orientation:

• morientation: Specifies the element material orientation.

• mbase: Specifies the material base (“old” method, deprecated).

morientation

morientation specifies the material orientation. This can be done in one of several ways. The morientation command is specified in the MDL elements block.

MDL Specification

morientation
   parameters
end

The first way is to specify a base with two vectors, from which an orthogonal reference frame is constructed (the base specified base vectors do not need to be orthogonal, but they must not be co-linear). The following operations are optional: The reference frame can be rotated about one of its axes. One of the axes can then be projected onto the element reference surface to construct an orthogonal reference frame whose Z-axis is aligned with the element normal. Finally, the reference frame can be rotated again about its Z-axis:

morientation
    base u1 u2 u3  v1 v2 v3
    rotate axis X|Y|Z angle a # optional
    project axis X|Y|Z]  # optional
    rotate angle a # optional
end

The second way specifies a transformation, from which an orthogonal reference frame for the coordinates of the element integration point is calculated. The following operations are optional: The reference frame can be rotated about one of its axes. One of the axes can then be projected onto the element reference surface to construct an orthogonal reference frame whose Z-axis is aligned with the element normal. Finally, the reference frame can be rotated again about its Z-axis:

morientation
    transformation id
    rotate axis X|Y|Z angle a # optional
    project axis X|Y|Z # optional
    rotate angle a # optional
end

The third way specifies a vector which is projected onto the reference surface (which is defined by the element-local X- and Y-axes), to construct an orthogonal reference frame whose Z-axis is aligned with the element-local Z-axis. This reference frame can then be rotated about the Z-axis:

morientation
    vector u1 u2 u3
    rotate angle a # optional
end

Another possibility is to use the element-local reference frame as calculated at the element integration point. This reference frame can be rotated about the Z-axis:

morientation
    element
    rotate angle a # optional
end

The rotation angles are specified in degrees. When using laminate materials, a final rotation about the ply angle performed automatically. For the projection, it is necessary that the projected axis or vector is not co-linear with the shell surface normal.

To visualize the material orientations as calculated at the element integration points, an analysis (for example linear) must be performed with the gradients parameter set to 1. This will write the dataset MBASE_IP to the database which can be visualized with baspl++ usig the following script:

if len(sys.argv) != 2:
    print 'usage: baspl++ %s database' % sys.argv[0]
    sys.exit(1)

 m = Model(sys.argv[1])
 p = NPart(m)
 p.face.show = False
 p.edge.show = True
 p.elements.extract = 1
 f = Field(m, 'MBASE_IP', case_index=0, cycle_index=0)
 p.sampling.field = f

mbase

“Old” method for specifying the material reference coordinate system. Please make use of the morientation method instead.

MDL Specification

mbase flag e11 e12 e13 e21 e22 e23 e31 e32 e33

mbase specification

flag	Description
0	The material reference coordinate system is identical to the branch coordinate system. The base vectors e11 e12 e13 e21 e22 e23 e31 e32 e33 are then dummy vectors, but must be specified with dummy float values.
1	Thematerial reference coordinate system is defined by base vectors e11 e12 e13 e21 e22 e23 e31 e32 e33 with respect to the branch coordinate system.
2	The material reference coordinate system is defined by base vectors e11 e12 e13 e21 e22 e23 e31 e32 e33 with respect to the element-local coordinate system.
3	The material reference coordinate system is defined by base vectors e11 e12 e13 e21 e22 e23 e31 e32 e33 with respect to the integration point local coordinate system.
12	The material reference coordinate system is defined by angles of orientation (Euler angles) e11 e12 e13 with respect to the element-local coordinate system. The remaining values e21 e22 e23 e31 e32 e33 are then dummy values, but must be specified with dummy float values.
13	The material reference coordinate system is defined by angles of orientation (Euler angles) e11 e12 e13 with respect to the integration point local coordinate system. The remaining values e21 e22 e23 e31 e32 e33 are then dummy values, but must be specified with dummy float values. Note that the default element material reference coordinate system is element-dependent, see Generic Elements.

Integration Schemes

All B2000++ elements requiring numerical integration have a built-in default integration rule. The default integration rule can be changed with the ischeme element parameter.

The type of integration rule depends on the element type (for example, integration rules for triangles cannot be applied to quadrilateral elements). The command ischeme default sets the default integration rule.

Optional MDL Parameters

ischeme type

Specifies the integration rule to be selected for subsequently specified elements. An appropriate integration rule is chosen by default, which can be overridden by ischeme. type is one of:

default

Resets the integration scheme to the default value for the selected element type.

TETRAn

Integration rule for tetrahedral elements, where the integration order n is one of 1, 2, 3, 4, 5, 6, and designates the maximum order to which monomials can be integrated exactly:

\[\iiint x^{a}y^{b}z^{c} dx dy dz\quad;\quad a + b + c \leq o\]

The number of integration points is 1, 4, 5, 14, 15, 24, respectively.

GAUSSn1[Xn2[Xn3]] | GLLn1[Xn2[Xn3]]

n1*n2*n3 point Gauss-Legendre or Gauss-Legendre-Lobatto tensor-product integration rules for line elements, quadrilateral elements, and hexahedral elements, respectively. n1, n2, and n3 (1-32) define the maximum order of integration in each element’s element-internal direction \(o_{i} = 2n_{i} - 1\) and \(o_{i} = 2n_{i} - 3\) for Gauss-Legendre and Gauss-Legendre-Lobatto, respectively.

Due to the limited numerical precision of the 64bit CPUs (15-16 decimal places), Gauss-Legendre and Gauss-Legendre-Lobatto integration rules with 1 greater than 15 are inaccurate, the error increasing with the number of integration points.

TRIANGo_GAUSSx and TRIANGo_GLLn

Tensor-product integration rule for prism elements, where x is one of 1-20 and designates the order to which monomials can be integrated exactly in-plane, and n is the number of integration points for the GAUSS or GLL rule in vertical direction.

Example

Define 3 by 3 Gauss integration rule for element 1 and a 4 by 4 Gauss-Legendre-Lobatto rule for element 2. Element is reset to the default rule.

elements
  eltype Q4.S.2D.TL
  mid 1
  ischeme GAUSS3X3
  1  1 2 5 6
  ischeme GLL4X4
  2  2 3 6 7
  ischeme default
  3  3 4 7 8
end

Footnotes

[1] (1,2,3,4,5,6)

Degrees Of Freedom components.

[2] (1,2,3,4,5,6,7,8,9)

Sampling Point Field or element-local derived components.